[Mano의 컴퓨터시스템구조] 디지털 논리회로 - 디지털 컴퓨터, 논리 게이트, 불 대수

Posted: 2024.11.25     Updated: 2024.11.25

컴퓨터 구조 스터디를 하며 ‘Mano의 컴퓨터시스템구조 제3판’ 교재를 정리한 글입니다.

디지털 컴퓨터

디지털(digital)

컴퓨터 내부 정보가 제한된 수의 불연속적인 값으로 표시된다는 것이다.
(* digit: 숫자, 숫자 기호)

초기의 전자 디지털 컴퓨터들은 십진수를 사용하여 산술 계산을 수행했다.
여기서 디지털 컴퓨터라는 용어가 생겨났다.

인간의 논리가 참 또는 거짓, 예 또는 아니오로 이진적이므로, 디지털 시스템들이 두 개의 값만 가지도록 제한되었다.
이를 이진수(binary)라고 한다.

이진수

하나의 이진 숫자를 비트(bit)라고 부른다.

디지털 컴퓨터에서의 정보는 비트들의 그룹으로 표현된다.
비트 그룹은 같은 비트 그룹일지라도 여러가지 다른 의미로 사용될 수 있다.
때에 따라 영문자나 다른 제어 신호를 나타낼 수 있다.

2의 거듭제곱을 통해 이진수와 십진수를 서로 변환할 수 있다.

• 1001011을 십진수로 변환

\[1 \times 2 ^6 + 1 \times 2 ^3 + 1 \times 2 ^1 + 1 \times 2 ^0 = 75\]

오른쪽부터 2의 0제곱, 2의 1제곱 순서대로 1 또는 0과 곱하여 합산한다.

하드웨어와 소프트웨어

하드웨어

컴퓨터의 모든 전자 부품과 주변 장치를 구성하는 전자기적 부품들이다.

소프트웨어

컴퓨터의 다양한 정보 처리 작업을 수행하는 명령어와 데이터들로 구성되어 있다.

컴퓨터의 연속된 명령어들을 프로그램이라고 한다.

시스템 소프트웨어

운영체제(Operating System)라고 하는 컴퓨터 시스템을 효율적으로 사용하기 위한 목적의 프로그램 집합이다.

시스템 소프트웨어는 사용자 응용 프로그램과는 다르다.

예를 들어 특정 목적을 위하여 작성된 고급 언어 프로그램은 응용 프로그램에 속하고, 이 프로그램을 기계어로 바꿔주는 컴파일러는 시스템 프로그램이다.

컴퓨터 하드웨어는 복잡하므로, 사용자가 복잡한 동작 원리를 알지 못하더라도 사용할 수 있도록 하기 위함이다.

하드웨어

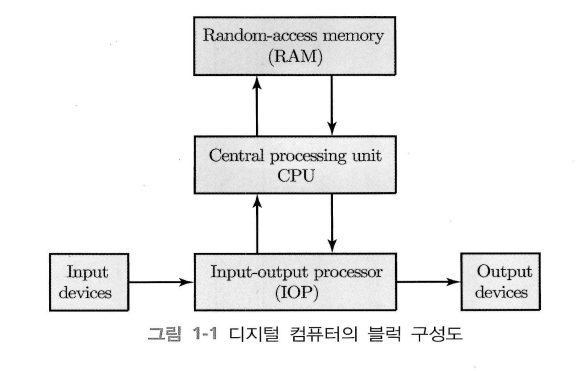
컴퓨터 하드웨어는 세 가지 부분으로 나뉜다.

RAM

• 임의 접근 기억 장치(Random Access Memory)이다.
• 명령어와 데이터를 저장하고 있다.
• CPU가 이진 정보를 입력하거나 가져올 때 어느 위치에 저장된 데이터든 항상 일정한 시간이 소요된다.
• 데이터를 임의의 위치에서 바로 읽거나 쓸 수 있는 메모리이다.

CPU

• 중앙 처리 장치(Center Processing Unit)이다.
• 데이터를 조작하는 산술 및 논리 연산 부분, 데이터를 저장하는 여러 개의 레지스터, 명령어를 가져와 수행하는 제어 회로 등이 들어 있다.

IOP

• 입출력 프로세서(Input Output Processor)이다.
• 외부와 통신, 데이터 전송을 제어하는 부분이다.
• 입출력 장치에는 키보드, 프린터, 터미널, 자기 디스크 장치(HDD) 등이 있다.

하드디스크는 데이터를 읽고 쓰는 과정에서 입출력을 수행하므로, 보조 기억장치이면서 입출력 장치이다.

컴퓨터 하드웨어의 연구 관점

컴퓨터 조직

하드웨어 구성품들의 동작 방식과 연결 방식에 관점을 둔다.
각 구성품들이 제대로 동작하기 위한 조직적 구조를 연구한다.

컴퓨터 설계

컴퓨터 하드웨어를 설계하는 것이다.
하드웨어 입장에서 컴퓨터를 구현하고, 제시된 컴퓨터 사양에 따라 적절한 하드웨어를 선택하고 연결 방식을 결정하여 시스템을 개발한다.

컴퓨터 구조

사용자의 입장에서 컴퓨터의 구조나 동작에 관점을 둔다.
정보의 형식, 명령어 집합, 메모리 기법 등을 연구한다.

논리 게이트

컴퓨터에서 이진 정보는 물리량인 전압 신호를 통해 0과 1을 표현한다.
예를 들어 3v 신호를 1, 0.5v 신호를 0으로 나타낼 수 있다.

게이트(gate)

이진 정보를 처리하는 논리 회로이다. 입력 논리의 필요 조건을 만족하면 1 또는 0 신호를 만든다.

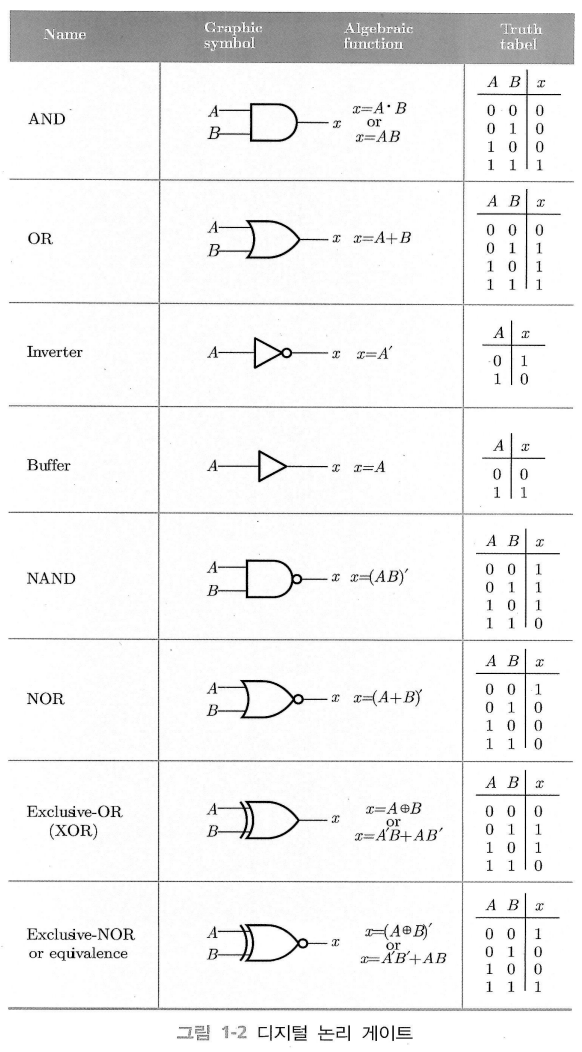
왼쪽부터 여러 종류의 게이트의 이름, 기호, 대수 표현식, 진리표이다.

논리 표현식의 ' 표시와 기호 표시의 작은 원은 인버터(inverter), 보수(complement)를 의미한다.

불 대수(Boolean Algebra)

19세기 수학자 George Boole에 의해 개발되었다.
0, 1 또는 참(True), 거짓(False)를 표현하고 연산에 사용한다.
이진 변수와 논리 동작을 취급하는 대수이다.
$A$, $B$, $x$, $y$ 등 문자로 표기한다.

불 대수는 디지털 회로의 해석과 설계를 쉽게 하기 위해 사용한다.

변수 사이의 진리표 관계, 논리도의 입출력 관계를 대수 형식으로 표현하고, 더 간단한 회로를 발견하기 위함이다.

주요 연산

1. AND(논리곱)

2. OR(논리합)

3. NOT(부정, 보수)

불 대수의 기본 관계

(1)~(8): 단일 변수 사이의 기본 관계
(9)~(13): 보통의 대수와 비슷
(14): 보통 대수 식에서는 적용되지 않음
(15), (16): De Morgan 정리
(17): 어떤 변수가 두 번 보수화되면 자기 자신이 됨

드모르간 정리 (De Morgan 정리)

• AND 연산에 대한 부정은 각 항목의 부정을 OR 연산으로 결합한 것과 같다.

\[(x+y+z)'=x'y'z'\]

• OR 연산에 대한 부정은 각 항목의 부정을 AND 연산으로 결합한 것과 같다.

\[(xyz)' = x'+y'+z'\]

불 대수가 디지털 회로에 적용되는 예시

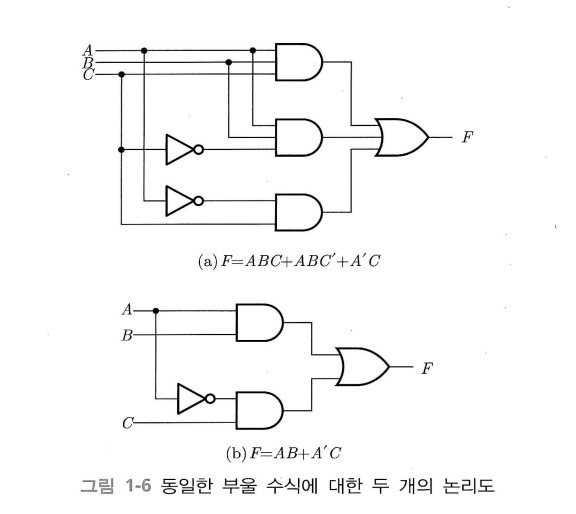
위의 그림을 보면 회로의 출력은 아래와 같다.

\[F = ABC+ABC'+A'C\]

불 대수를 적용하여 아래와 같이 식을 간소화할 수 있다.

\[\begin{align*} F &= ABC + ABC' + A'C \\ &= AB(C + C') + A'C \\ &= AB + A'C \end{align*}\]

수식의 보수

드모르간 정리를 이용하여 어떠한 수식 F의 보수를 얻을 수 있다.
수식에서 모든 OR 연산은 AND로, 모든 AND 연산은 OR로 바꾸고, 각 변수를 보수화한다.

\[F = AB + C'D' + B'D \\ F' = (A' + B')(C + D)(B + D')\]