[Mano의 컴퓨터시스템구조] 디지털 논리회로 - 맵의 간소화, 조합 회로
Posted: Updated:
컴퓨터 구조 스터디를 하며 ‘Mano의 컴퓨터시스템구조 제3판’ 교재를 정리한 글입니다.
맵의 간소화
카르노 맵 (Karnaugh map)
진리표로 논리 표현식을 얻을 수 있으며, 논리 표현식은 불 대수로 간단하게 만들 수 있다.
카르노 맵(Karnaugh map)은 불 함수를 간소화할 수 있는 방식이다.
민텀(minterm): 진리표에서 변수의 각 조합, $n$ 개 변수가 있으면 $2^n$ 개의 민텀이 있게 됨
아래와 같은 불 함수가 있다고 할 때,
\[F = x + y'z\]진리표와 논리도는 아래와 같다.
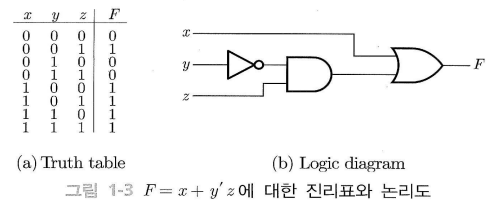
여기서 출력 $F$ 가 1이 되는 민텀을 뽑으면 아래 식과 같다.
\[\begin{align*} F(x, y, z) &= \sum (1, 4, 5, 6, 7) \\ &= x'y'z+xy'z'+xy'z+xyz'+xyz \end{align*}\]$\sum (1, 4, 5, 6, 7)$ 은 진리표의 1, 4, 5, 6, 7번째 민텀의 논리합이다.
(진리표의 순번은 0부터 시작한다)
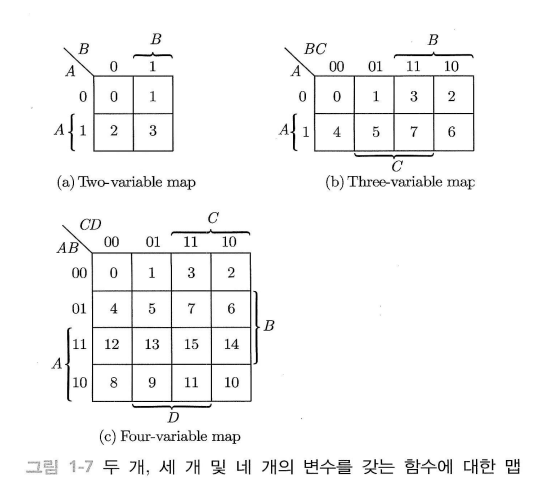
카르노 맵은 2변수 카르노 맵, 3변수 카르노 맵, 4변수 카르노 맵이 있다.
각 칸에 적힌 숫자는 진리표의 민텀 번호를 의미한다.
논리 표현식의 결과가 1이면 해당하는 민텀 칸에 1을 적고, 0이면 0을 적는다.
각 변수는 보통 A, B, C, D로 나타내며, 2변수 카르노 맵에서는 행이 A이고 열이 B, 3변수 카르노 맵에서는 행이 A이고, 열이 BC, 4변수 카르노맵에서는 행이 AB이고, 열이 CD이다.
위 이미지에서는 각 변수가 1이 되는 위치가 { 기호로 표시되어 있다.
바이트 코드 순서는 이진수 순서대로 나타낸 진리표와 다르게 그레이 코드로 작성되어 있다.
00 01 11 10 처럼 양옆의 비트와 1만 차이나도록 작성된 것이 그레이 코드(gray code)이다.
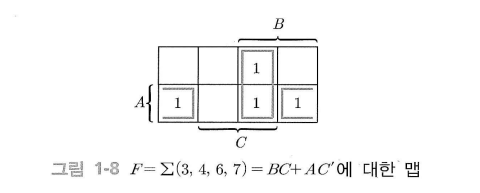
진리표에 의해 표시되는 불 함수에서 출력이 1인 민텀 구역에 1을 표기한다.
그리고 인접한 1을 $2^n$ 개수만큼, 즉 2개, 4개, 8개씩 가능한 크게 묶는다.
위 그림처럼 양 옆으로 떨어져 있어 보이는 것도 함께 묶는다.
묶인 그룹에서는 각 민텀이 가진 변수 중에서 중첩된 변수만 남기고 지우면 된다.
예를 들어, 3번째 민텀과 7번째 민텀 $A’BC$ (011)와 $ABC$ (111)를 보면, $A$ 는 $A’$ (0)와 $A$ (1)로 서로 다르므로 지운다.
$B$ (1)와 $C$ (1)는 동일하므로 남겨두고, 이 그룹의 결과는 $BC$가 된다.
이런 방식으로 모든 그룹을 계산하여 논리합(OR)을 취한다.
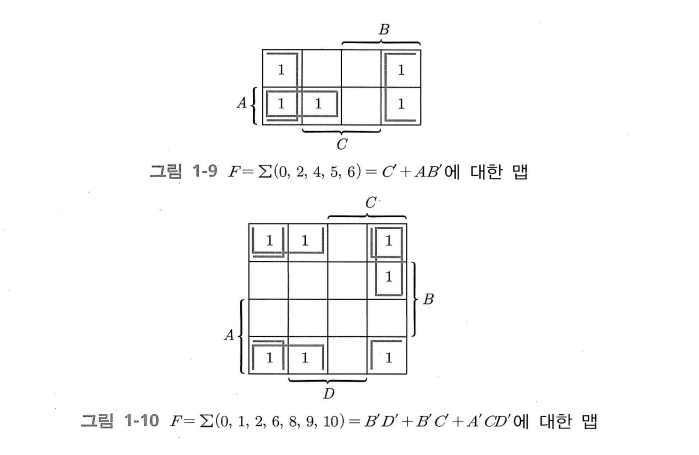
3변수 카르노 맵에서는 그림 1-9와 같이 양 옆에 있는 민텀도 이어져 있다고 치므로 묶을 수 있다.
4변수 카르노 맵에서는 그림 1-10과 같이 상하좌우 모서리를 포함하여 끝쪽에 있는 민텀도 이어져 있다고 치므로 묶을 수 있다.
논리합의 논리곱
앞에서 계산한 방식은 논리곱의 논리합(sum of products) 방식이다.
그룹을 묶어 AND 연산 후 각 그룹을 OR 연산한다.
경우에 따라 논리합의 논리곱(product of sums) 방식을 사용할 수도 있다.
이 방식을 사용할 때는 전과 반대로 출력이 0인 민텀 구역에 0을 표기하고 가능한 크게 묶는다.
결과물은 $F’$ 이 되므로, 드모르간 정리에 의해 $ F = (F’)’ $ 를 얻을 수 있다.
Don’t Care 조건
1을 표기하는 논리곱의 논리합, 0을 표기하는 논리합의 논리곱 둘 중 어느 방식이든 민텀이 1이거나 0이거나 관계 없는 don’t care 를 가지는 경우가 있다.
최적의 간소화를 위해 필요할 경우 X로 표기하여 이를 1로 보거나 0으로 보도록 하여 함께 묶을 수 있다.
F라는 불 함수가 있을 때, $d(A, B, C)$ 는 don’t care 조건이다.
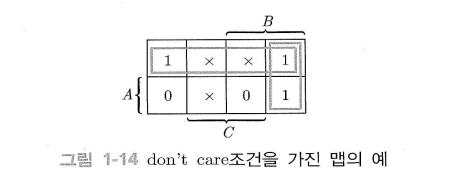
don’t care 조건을 전부 0으로 생각하여 묶으면 $ F = A’C’ + BC’ $ 로 간소화되고, 1로 보고 네 개의 민텀을 크게 묶는다면 $ F = A’ + BC’ $ 로 간소화할 수 있다.
조합 회로
현재 입력 값이 주어지면 이전 입력과 관계 없이 출력 값이 바로 나오는 회로이다.
반가산기
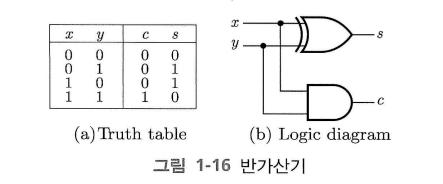
비트 두 개를 가산하는 조합회로이다.
위 그림은 두 개의 비트를 $x$ , $y$ 라고 할 때의 진리표이다.
$c$ 는 carry로 $x$ 와 $y$ 의 AND 연산과 같고, $s$ 는 합으로 $x$ 와 $y$ 의 XOR 연산과 같다.
전가산기
반가산기 두 개로 전가산기가 구성되며, 비트 두개와 밑의 자리로부터 올라오는 carry를 고려하여 비트 세 개를 가산한다.
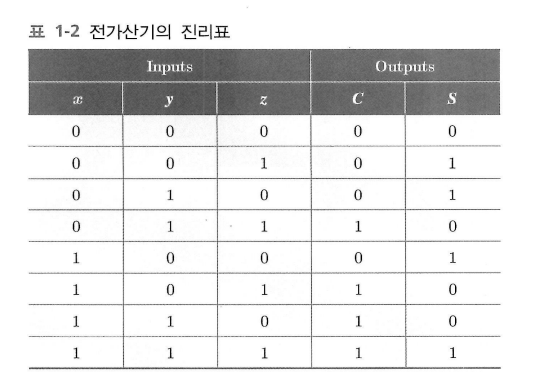
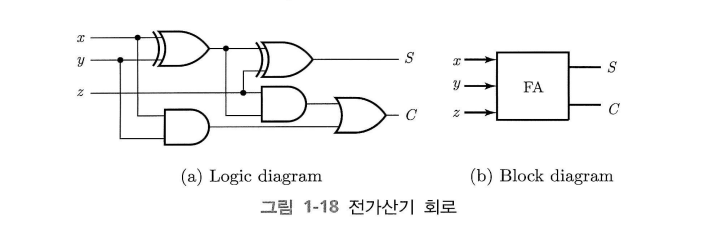
$z$ 는 밑의 자리에서 올라오는 캐리이고, $C$ 는 다음 자리로 올라가는 캐리이다.
$S$ 는 $x$ , $y$ , $z$ 의 XOR 연산이다.
$C$ 는 $x$ , $y$ 의 XOR 연산 후 $z$ 와 AND 연산한 뒤 $x$ 와 $y$ 의 AND 연산 값을 OR 연산한 것과 같다.

댓글남기기