[Mano의 컴퓨터시스템구조] 디지털 논리회로 - 순차 회로

Posted: 2024.12.18     Updated: 2024.12.18

컴퓨터 구조 스터디를 하며 ‘Mano의 컴퓨터시스템구조 제3판’ 교재를 정리한 글입니다.

순차 회로

게이트들로만 된 회로는 조합 회로이고, 플립플롭과 게이트를 연결하면 순차 회로가 된다.

플립플롭 입력식

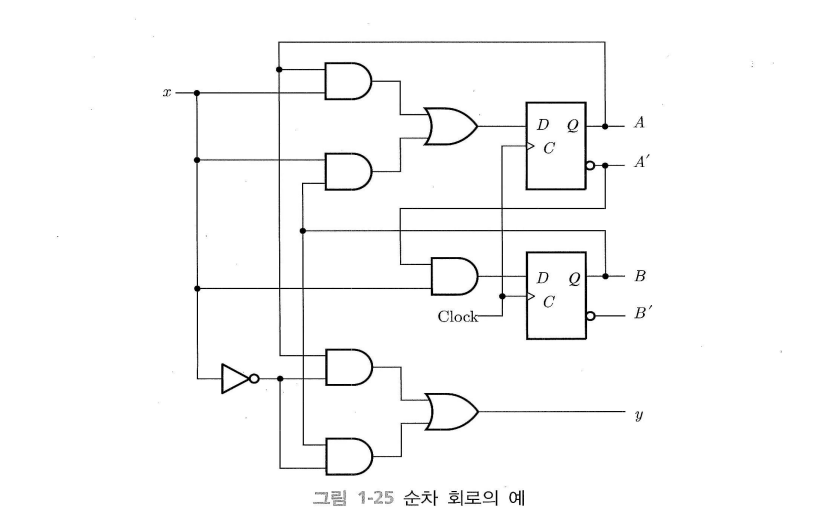
위의 순차 회로에서는 플립플롭의 입력을 조합 회로가 만들어낸다.
플립플롭의 입력 $D$를 플립플롭 입력식이라는 논리식으로 나타내면 아래와 같다.

\[D_A = Ax + Bx \\ D_B = A'x\]

입력 변수와 플립플롭 출력 사이의 관계에 따라 출력을 논리식으로 나타내면 아래와 같다.

\[y = Ax' + Bx'\]

상태표

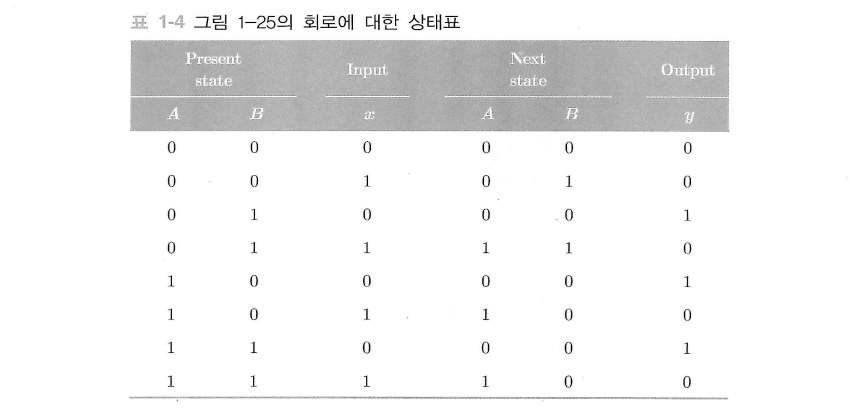
상태표는 순차 회로의 모든 가능한 현재 상태와 해당 상태에서의 입력값에 따라 결정되는 다음 상태와 출력을 나타낸다.

$m$개의 플립플롭, $n$개의 입력 변수, $p$개의 출력 변수를 가진 순차 회로의 경우,
현 상태에 $m$개의 열, 입력에 $n$개의 열, 다음 상태에 $m$개의 열, 출력에 $p$개의 행을 갖는 상태표가 된다.
행에는 $2^{m+n}$개의 조합이 나오게 된다.

상태도

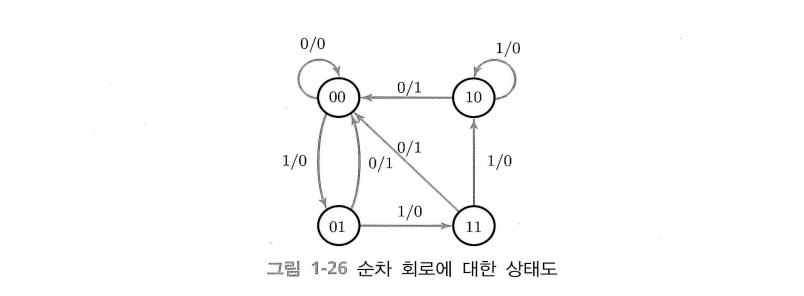
상태표에 나타난 정보를 그림으로 표시한 것이다.
상태는 원으로 표시하고, 상태 사이의 전이는 직선으로, 입출력 관계는 입력/출력 으로 표시한다.

상태 00에서 01로 가는 직선 위에 표시된 1/0 은 입력이 1이고 출력이 0일 때 현 상태 00에 있으며, 다음 클럭 펄스가 들어오면 회로가 다음 상태 01으로 간다는 의미이다.
원에서 나온 선이 다시 자신의 원을으로 들어가는 것은 상태 변화가 일어나지 않았다는 것이다.

상태표는 회로도로부터 쉽게 유도할 수 있고, 상태도는 상태표로부터 유도할 수 있다.

순차 회로 설계 과정

1. 회로 시방서(또는 회로 사양서, Circuit Specification) 확인
2. 상태도 그리기
3. 상태표 구하기
4. 회로도 획득

회로 시방서: 전자 회로 또는 시스템 설계 구현을 위한 요구사항을 정의한 문서

2비트 이진 카운터 설계하기

2비트 이진 카운터는 2비트 정보를 저장하고 이를 순차적으로 증가시키는 기능을 수행한다.
2개의 비트(A, B)를 사용하여 4가지 다른 상태를 나타낼 수 있고, 각 클록 펄스에 응답해 상태를 1씩 증가시킨다.
00에서 시작하여 01로, 다음은 10, 다음은 11로 변경되고, 이후에는 오버플로우하여 00으로 돌아간다.

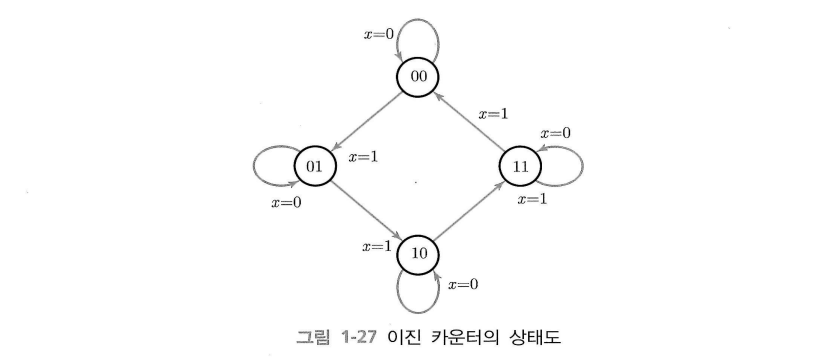
입력 $x$ 는 제어 변수로 외부 입력 $x=1$일 때 이진 상태 $00, 01, 10, 11, 00, \dots$ 를 반복한다.
$x=0$ 일 때는 회로의 상태는 변하지 않고 그대로 남는다.
각 상태가 2비트로 되어 있으므로 두 개의 플립플롭이 필요하다.

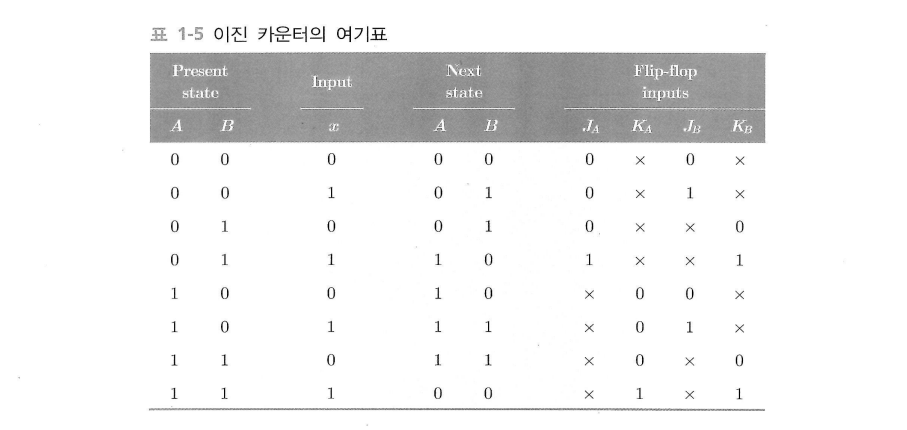
상태도를 통해 상태표를 구하고, 위 표에서 상태표는 처음 5열이다.
여기표는 상태표의 연장으로서 $JK$ 플립플롭을 사용해 설계되었다.

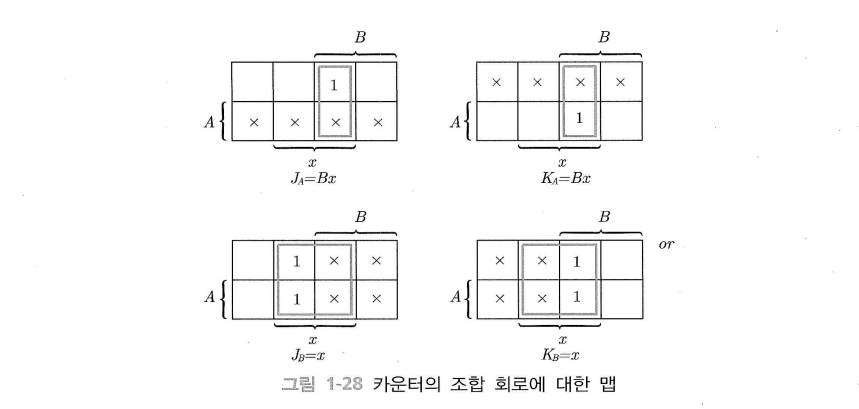
카르노 맵을 통해 간소화한 플립플롭의 입력조건을 구한 후에 회로를 구성하면 된다.
$A$, $B$, $x$ 를 변수로 하여 3변수 맵을 그린다.

• $A=0$, $B=1$, $x=1$일 때, $J_A=1$ 이고, $A$는 Don’t care 이므로 $J_A=Bx$이다.
• $A=1$, $B=1$, $x=1$일 때, $K_A=1$ 이고, $A$는 Don’t care 이므로 $K_A=Bx$이다.
• 상태와 관계 없이 $x$ 가 1이면 $J_B$ 가 1이므로 $J_B =x$이다.
• 상태와 관계 없이 $x$ 가 1이면 $K_B$ 가 1이므로 $K_B =x$이다.

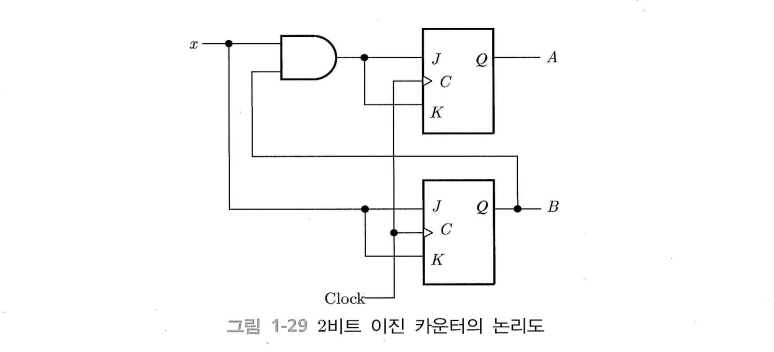
논리도를 그리기 위해 플립플롭을 먼저 그리고 모든 입력과 출력에 기호를 붙인다.
플립플롭 입력 함수의 논리식으로부터 조합 회로를 그린다.
플립플롭의 출력을 조합회로의 입력과 연결하고 조합회로의 출력을 플립플롭의 입력에 연결시킨다.