Better Jeong

Better Jeong

Vision Software Engineer

Posted:      Updated:

컴퓨터 구조 스터디를 하며 ‘Mano의 컴퓨터시스템구조 제3판’ 교재를 정리한 글입니다.

데이터의 표현

데이터의 종류

8진수, 16진수

컴퓨터에서 이진수와 8진수 변환, 이진수와 16진수 변환은 중요하다.

2816

이진수 비트를 밑의 비트부터 3비트씩 묶으면 8진수, 4비트씩 묶으면 16진수가 된다.

10진수

컴퓨터는 이진수, 사람은 십진수를 사용하므로, 십진수 입력을 이진수로 바꾸어 연산한 뒤 십진수로 바꾸어 출력한다.
컴퓨터 십진수를 이진화 십진수(BCD) 형태로 직접 계산할 수도 있는데, 한 자리당 4비트의 이진수로 바뀐다.

영자숫자의 표시

숫자, 영어 대소문자, 특수 기호 등을 표시하기 위해 7비트가 필요하다.
표준 코드는 ASCII(아스키) 코드를 많이 사용한다.

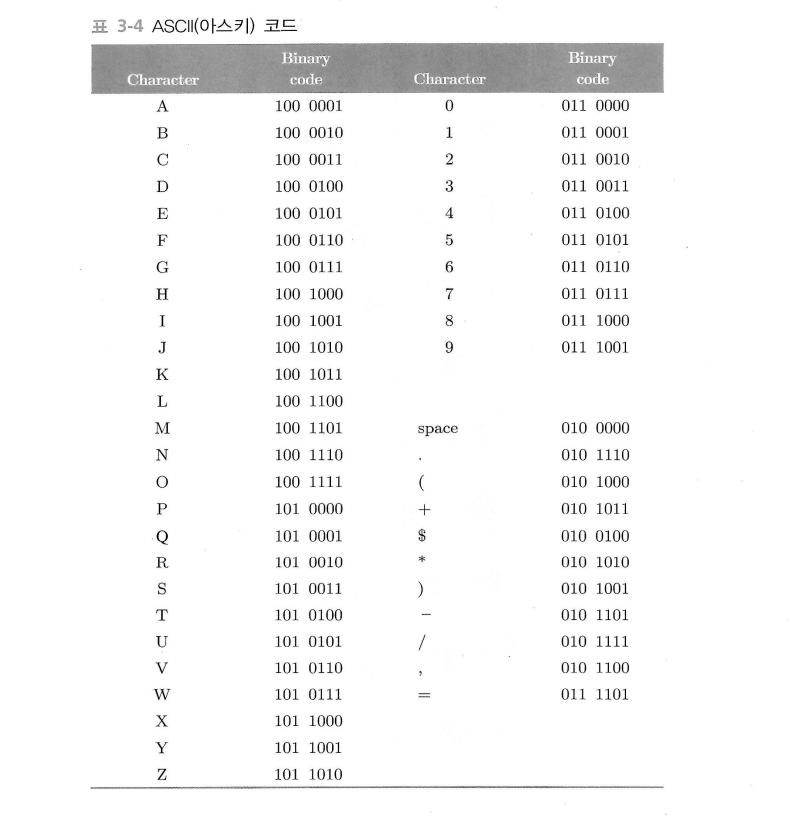
ascii

보수(complement)

디지털 컴퓨터에서 뺄셈 연산, 논리 계산에 사용된다.
$r$진법에는 $r$의 보수, $(r-1)$의 보수로 두 가지 종류의 보수가 있다.

$(r-1)$의 보수

십진수의 경우 $r$은 10이고, $r-1=9$이므로, $(10^n-1)-N$이다.
각 자리 숫자를 9에서 뺀 것과 같다.

ex) 546700에 대한 9의 보수: $999999-546700=453299$

이진수의 경우 $r=2$, $r-1=1$, $N$에 대한 1의 보수는 $(2^n-1)-N$이다.
각 자리 수를 1은 0으로, 0은 1로 바꾸어서 구할 수 있다.

8진수, 16진수도 마찬가지의 방식으로 계산한다.

$r$의 보수

$(r-1)$의 보수에 1을 더해서 얻을 수 있다.

\[r^n-N=[(r^n-1)-N]+1\]

ex) 십진수 2389에 대한 10의 보수: $7610+1=7611$
$\quad$ 이진수 101100에 대한 2의 보수: $010011+1=010100$

$N$이 소수점을 가지고 있을 경우, 일단 생략한 다음 보수를 구하고 적합한 위치에 소수점을 다시 붙인다.

어떤 수에 대한 보수를 다시 보수화하면 원래의 수로 되돌아간다.

부호 없는 숫자의 뺄셈

디지털 하드웨어에서 뺄셈을 계산할 때는 보수를 활용하는 것이 효율적이다.

$r$진수의 부호 없는 두 $n$자리수 사이의 뺄셈 $M-N$의 계산

  1. $M \ge N$인 경우
    1. $M$에 $N$에 대한 $r$의 보수를 더한다
    2. $end$ 캐리를 무시한다
  2. $M < N$인 경우
    1. $M$에 $N$에 대한 $r$의 보수를 더한다
    2. 더한 값에 대한 $r$의 보수를 구하고 $-$를 붙인다

고정 소수점 표현

숫자의 맨 왼쪽 비트를 부호 비트로 정하여 0은 양수, 1은 음수를 나타낸다.
부호 외에도 분수, 정수, 분수-정수 혼합된 수를 나타내기 위해 이진, 십진 소수점이 포함될 수 있다.

레지스터에서 이진 소수점을 나타낼 때, 고정 소수점 혹은 부동 소수점을 사용할 수 있다.

고정 소수점 방식

이진 소수점이 항상 동일한 위치에 존재

  1. 분수 표현: 레지스터의 맨 앞쪽에 둠
  2. 정수값 표현: 레지스터의 맨 오른쪽에 둠

첫 번째 레지스터에 저장된 숫자(소수점 위치)로 두 번째 레지스터에 저장된 숫자(실제 숫자 값)를 해석한다.

정수 표현

컴퓨터에서 정수는 양수와 음수로 나뉜다.
양수는 한 가지 방식으로 표현할 수 있지만, 음수는 3가지 표현 방식이 있다.

  1. 부호절대값(signed-magnitude) 표현
    • 가장 왼쪽 비트로 양수(0), 음수(1) 구분
  2. 부호화된 1의 보수(signed-1’s complement) 표현
    • 양수 숫자의 모든 비트를 반전해서 표현
  3. 부호화된 2의 보수(signed-2’s complement) 표현
    • 1의 보수에서 1을 더해서 표현

ex) 14와 -14 표현

  • 양수: 0 0001110
  • 음수
    • 부호절대값 표현: 1 0001110
    • 1의 보수 표현: 1 1110001
    • 2의 보수 표현: 1 1110010

컴퓨터에서는 산술 연산에 유리한 부호화된 2의 보수 표현을 사용한다.
1의 보수 표현은 0을 양수 0, 음수 0 두 가지 방식으로 표현할 수 있어 논리 연산에 사용된다.

산술 가산

두 수의 부호가 동일하면 절대값을 더한 후 부호를 붙이고, 두 수의 부호가 다를 경우 절대값이 큰 수에서 작은 수를 빼고 큰 수의 부호를 붙여준다.
따라서 두 수의 부호와 절대값을 비교하는 과정이 필요하다.

부호화된 2의 보수 표현에서는 덧셈과 보수화만으로 두 수의 덧셈을 계산한다.
부호를 포함하여 두 수를 더하고 부호 비트의 캐리는 무시한다.

산술 감산

음수가 2의 보수일 경우 부호 비트를 포함하여 감수의 2의 보수를 취하여 가산한다.

부호화된 2의 보수 형태의 이진수에 대한 덧셈과 뺄셈은 하나의 회로만으로 계산할 수 있다.
따라서 사용자나 프로그래머가 사용된 숫자를 보고 해석해야 한다.

오버플로

컴퓨터에서 메모리 레지스터를 포함하여 모든 레지스터에서 길이가 한정적이기 때문에 $n$비트 레지스터에 $n+1$비트 결과를 담지 못해 문제가 생긴다.
부호가 같은 두 수의 가산 결과에서 오버플로가 생길 수 있다.
부호가 다르면 원래의 수 중 큰 것보다 작아지므로 오버플로가 생길 수 없다.

오버플로가 생기면 컴퓨터가 오버플로 플립플롭을 세팅한다.

오버플로 조건: 부호 비트 밑에서 부호 비트로 올라온 캐리, 부호 비트로부터 생긴 캐리가 다름
두 캐리를 $exclusive-OR$ 게이트에 입력시켜 출력이 1이 되면 오버플로를 검출할 수 있다.

십진 고정 소수점 표현

BCD로 십진수를 나타내려면 각 자리 숫자마다 4개의 플립플롭이 사용되므로, 너무 많은 플립플롭이 사용되어 저장 공간이 낭비될 수 있다.
그러나 사람이 십진수를 사용하기 때문에 컴퓨터의 입출력으로 사용된다.
BCD로 입력한 후 이진수로 변환하여 연산 수행 후 BCD로 변환하여 출력할 수도 있지만, 대부분의 컴퓨터는 BCD 형태의 십진수를 직접 계산할 수 있다.

BCD에서는 부호절대값 표현, 부호화된 보수 표현을 모두 사용할 수 있다.
0은 양수에 대한 부호, 9(1001)은 음수에 대한 부호이다.
덧셈과 뺄셈은 이진수에서와 같은 방식으로 진행한다.

부동 소수점 표현

\[m \times r^e\]

가수($m$, mantissa): 부호화된 고정 소수점 숫자
지수($e$, exponent): 십진 또는 이진 소수점의 위치를 알려주는 부분

레지스터에서 $m$과 $e$는 부호를 포함해서 저장한다.
밑수 $r$과 가수의 소수점은 가정되어 있다고 간주한다.

부동 소수점 숫자의 산술 연산 시 고정 소수점보다 복잡하고 시간이 많이 걸린다.
매우 큰 수와 작은 수를 표시하기에는 편리하다.

십진수 $+6132.789$의 표현

$Fraction$: $+0.6132789$
$Exponent$: $+04$
실제 소수점이 분수의 소수점에서 오른쪽으로 네 번 이동한 곳에 위치함
따라서, $+0.6132789 \times 10^{+4}$와 같음

이진수 $+1001.11$의 표현

8비트 분수와 6비트 지수를 이용하여 나타낸다.

$Fraction$: $01001110$
$Exponent$: $000100$

\[m \times 2^e = +(.1001110)_2 \times 2^{+4}\]

정규화

부동 소수점 숫자에서 최상위 비트가 0이 아닌 경우이다.
정규화된 숫자는 부동 소수점 표현에서 가장 높은 정밀도를 제공한다.

댓글남기기