[Mano의 컴퓨터시스템구조] 레지스터 전송과 마이크로 연산
Posted: Updated:
컴퓨터 구조 스터디를 하며 ‘Mano의 컴퓨터시스템구조 제3판’ 교재를 정리한 글입니다.
레지스터 전송과 마이크로 연산
레지스터 전송 언어
마이크로 연산(micro-operation)
하나의 클럭 펄스 동안 실행되는 기본 동작이다.
- 시프트(shift)
- 카운트(count)
- 클리어(clear)
- 로드(load)
레지스터 전송 언어(register transfer language)
레지스터 간 마이크로 연산 전송을 간단하고 명료하게 표시하기 위해 사용하는 기호이다.
레지스터 전송
MAR: 메모리 주소 레지스터 (memory address register)
PC: 프로그램 카운터 (program counter)
IR: 명령어 레지스터 (instruction register)
R1: 프로세서 레지스터 (processor register)
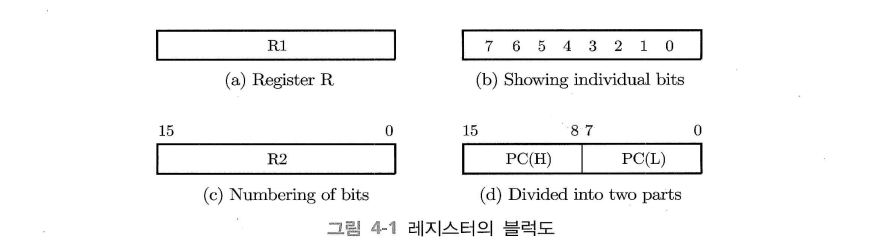
사각형 안에 이름을 적어 레지스터를 나타낸다.
$n$ 비트 레지스터의 각 플립플롭들은 맨 오른쪽을 0으로 하고 $n-1$까지 번호가 매겨진다.
PC의 경우 두 파트로 나눠진 16비트 레지스터로 0-7은 하위 바이트($L$), 8-15는 상위 바이트($H$)이다.
$\leftarrow$: 치환 연산자, 레지스터들 사이의 정보 전송을 나타냄
\[If(P = 1) \quad then (R2 \leftarrow R1)\] \[= P: R2 \leftarrow R1\]$if-then$ 문장: 레지스터 전송이 정해진 제어 조건일 때만 발생하도록 함
제어 함수: 0 또는 1을 가지며, $P=1$일 때 전송 수행
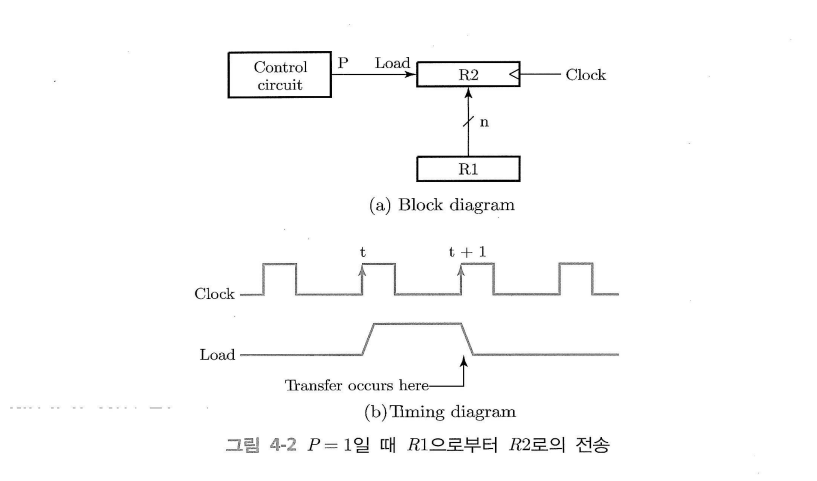
(a) 에서 $R1$의 $n$비트 레지스터 출력이 $R2$의 입력으로 연결되어 있다.
Load 신호가 상승하면 다음 클록 펄스가 상승할 때 데이터 전송이 이루어진다.
$P$ 는 시간 $t$ 에 활성화되며, 매 클럭 변이에서 전송이 일어나는 것을 막기 위해 $t+1$에 0으로 돌아간다.
레지스터 전송에 사용되는 기본 기호
| Symbol | Description | Examples |
|---|---|---|
| Letters (and numerals) | Denotes a register | MAR, R2 |
| Parentheses ( ) | Denotes a part of a register | R2(0–7), R2(L) |
| Arrow ← | Denotes transfer of information | R2 ← R1 |
| Comma , | Separates two microoperations | R2 ← R1, R1 ← R2 |
레지스터: 영어 대문자, 숫자로 표현 ex) MAR, R2
레지스터 일부: 괄호()를 사용해 비트 범위, 부분 혹은 레이블 표시 ex) (0-7), (L)
화살표: 전송 방향
쉼표: 동시에 일어나는 동작
버스와 메모리 전송
각 레지스터가 독립된 라인을 사용하게 되면 숫자가 너무 많아지므로, 버스(bus) 시스템을 공통으로 사용한다.
버스는 한 번에 하나의 전송이 이루어지도록 사용할 레지스터를 선택한다.
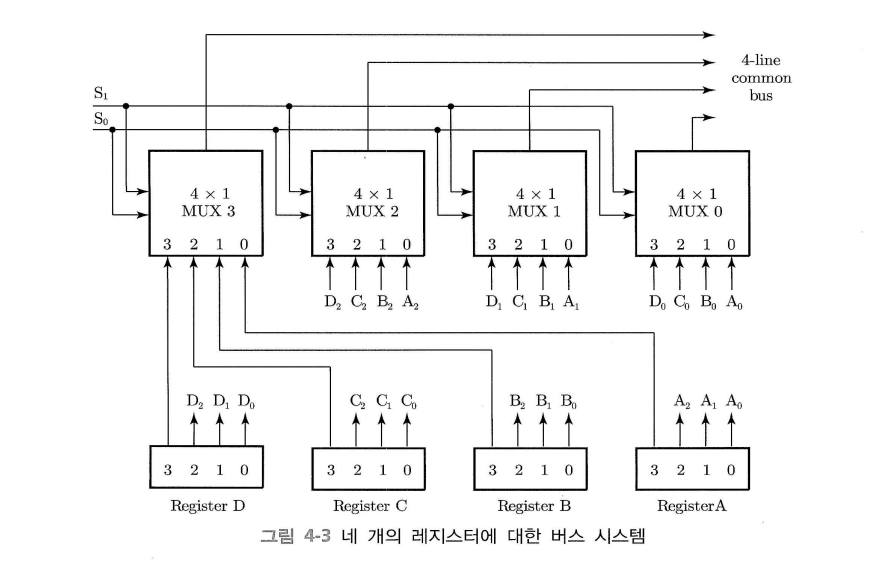
멀티플렉서를 이용하여 공통 버스를 구성할 수 있다.
0-3 네 개의 비트를 가진 각 레지스터에서 동일한 위치의 비트가 하나의 멀티플렉서에 연결된다.

$S_1S_0=00$ 일 때, 각 레지스터의 0번 비트를 선택하므로 레지스터 A가 선택된다.
01, 10, 11일 때는 각각 1번, 2번, 3번 비트를 선택하게 된다.
$n$비트의 $k$ 레지스터를 멀티플렉스하는 버스 시스템에서는 $n$개의 $k \times 1$ 멀티플렉서가 필요하다.
위는 4비트의 4개 레지스터에 대한 버스 시스템이므로 4개의 $4 \times 1$ 멀티플렉서가 사용됐다.
16비트의 8개 레지스터에 대한 버스는 16개의 $8 \times 1$ 멀티플렉서와 3개의 선택 입력이 필요하다.
레지스터 전송문에 버스를 포함하여 표현했다.
버스가 시스템에 존재한다는 가정 하에 생략할 수 있다.
3-상태 버스 버퍼
멀티플렉서 대신 3-상태 게이트를 사용하여 구성한 버스 시스템이다.
3가지 상태는 각각 논리 0, 1과 고저항 상태(high-impedance state)이다.
고저항 상태: 개회로와 마찬가지로 출력이 차단되어 아무 논리값도 가지지 않음
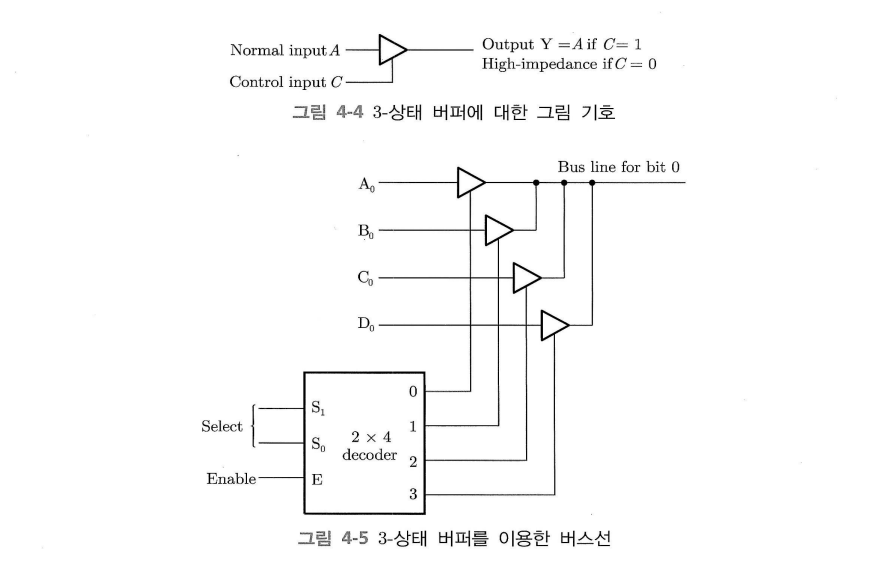
디코더의 인에이블 입력이 0이면 모든 버스 라인이 고저항 상태가 된다.
반면 인에이블 입력이 1일 경우 디코더 입력값에 따라 하나의 버퍼만 활성화된다.
제어 입력이 1일 경우 출력이 입력과 동일한 값을 가지고, 0일 때는 고저항 상태이다.
메모리 전송
메모리에서 정보를 가져올 때는 읽기(read) 동작이라 하고, 정보를 저장할 때는 쓰기(write) 동작이라고 한다.
메모리 워드는 $M$으로 나타낸다.
메모리를 주소 레지스터(Address register, AR)로부터 받아 데이터 레지스터(data register, DR)에 전송하는 읽기 동작을 나타낸 기호이다.
\[Wirte: M[AR] \leftarrow R1\]레지스터 R1에 있는 데이터를 $AR$에 지정된 메모리 주소에 전송하는 쓰기 동작을 나타낸 기호이다.
산술 마이크로 연산
덧셈, 뺄셈, 인크리멘트, 디크리멘트, 시프트 등이 있다.
곱셈, 나눗셈 연산은 산술 연산이지만 기본 연산 집합에는 포함되지 않는다.
곱셈: 여러 개의 덧셈, 시프트 마이크로 연산으로 구현
나눗셈: 여러 개의 뺄셈, 시프트 마이크로 연산으로 구현
| 기호적 표현 | 설명 |
|---|---|
| $R3 \leftarrow R1 + R2$ | $R1$과 $R2$의 합을 $R3$에 저장 |
| $R3 \leftarrow R1 - R2$ | $R1$에서 $R2$를 뺀 값을 $R3$에 저장 |
| $R2 \leftarrow \overline{R2}$ | $R2$의 보수를 구하여 저장 (1의 보수) |
| $R2 \leftarrow \overline{R2} + 1$ | $R2$의 2의 보수를 구하여 저장 (부호 반전) |
| $R3 \leftarrow R1 + \overline{R2} + 1$ | $R1$과 $R2$의 2의 보수를 더해 $R3$에 저장 (뺄셈) |
| $R1 \leftarrow R1 + 1$ | $R1$의 값을 1 증가 |
| $R1 \leftarrow R1 - 1$ | $R1$의 값을 1 감소 |
- $\overline{R2}$는 $R2$에 대한 1의 보수이고, $\overline{R2} + 1$은 $R2$에 대한 2의 보수이다.
- $R3 \leftarrow R1 - R2$ = $R3 \leftarrow R1 + \overline{R2} + 1$
마이크로 연산의 종류
- 레지스터 전송 마이크로 연산: 레지스터 사이에서 이진 정보 전송
- 산술 마이크로 연산: 레지스터에 저장된 수치 데이터에 산술 연산 수행
- 논리 마이크로 연산: 레지스터에 저장된 비수치 데이터에 비트 조작 연산 수행
- 시프트 마이크로 연산: 레지스터에 저장된 데이터에 시프트 연산 수행
이진 가산기
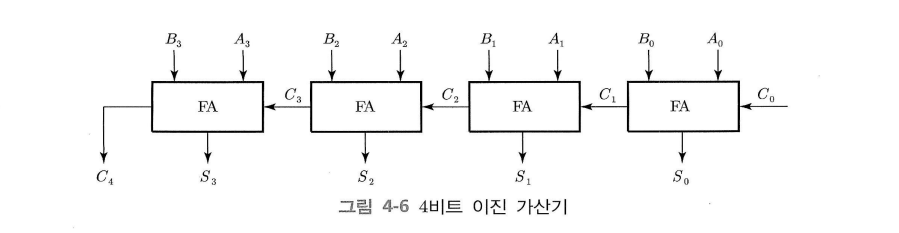
전가산기(full-adder): 두 비트와 이전 캐리의 산술 합 계산
이진 가산기(binary adder): 임의의 길이의 두 이진수에 대한 덧셈 수행
이진 가산기는 여러 개의 전가산기들을 직렬로 연결하여 이전 캐리 출력이 다음의 캐리로 입력되게 구성한다.
이진 감가산기
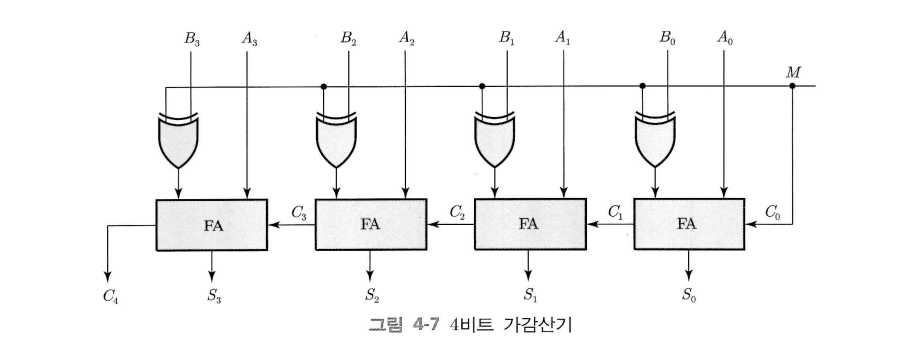
이진수의 뺄셈은 2의 보수를 이용한 덧셈으로 계산한다.
XOR 게이트(같으면 0, 다르면 1)를 활용해 덧셈과 뺄셈 연산을 하나의 회로로 구현할 수 있다.
모드(mode)입력 $M$이 0이면 가산기, 1이면 감산기로 동작한다.
XOR 게이트를 활용하였으므로 $M = 0$일 때 $B = 0$이면 0 입력, $B = 1$이면 1이 입력되므로 원래의 $B$가 그대로 입력된다.
반대로 $M=1$일 때 $B=0$이면 1, $B=1$이면 0이 입력되므로 $B’$이 된다.
여기서 $M=1$이면 $C_0$가 1이므로, B에 대한 2의 보수(1의 보수+1)가 입력되는 것과 같다.
이진 인크리멘터
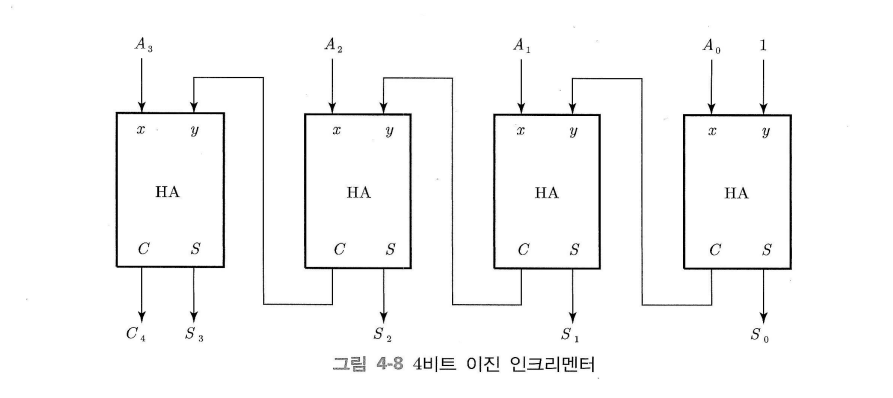
레지스터의 값에 1을 더하는 연산이다.
최하위 비트의 입력이 논리 1이며, 캐리가 다음 반가산기의 입력에 연결되어 $A_0$에서 $A_3$까지의 입력을 1 증가시켜 $S_0$ ~ $S_3$ 출력을 만들어낸다.
입력된 이진수가 1111이면 출력 캐리($C_4$)가 1이 되고 출력은 0이다.
산술 회로
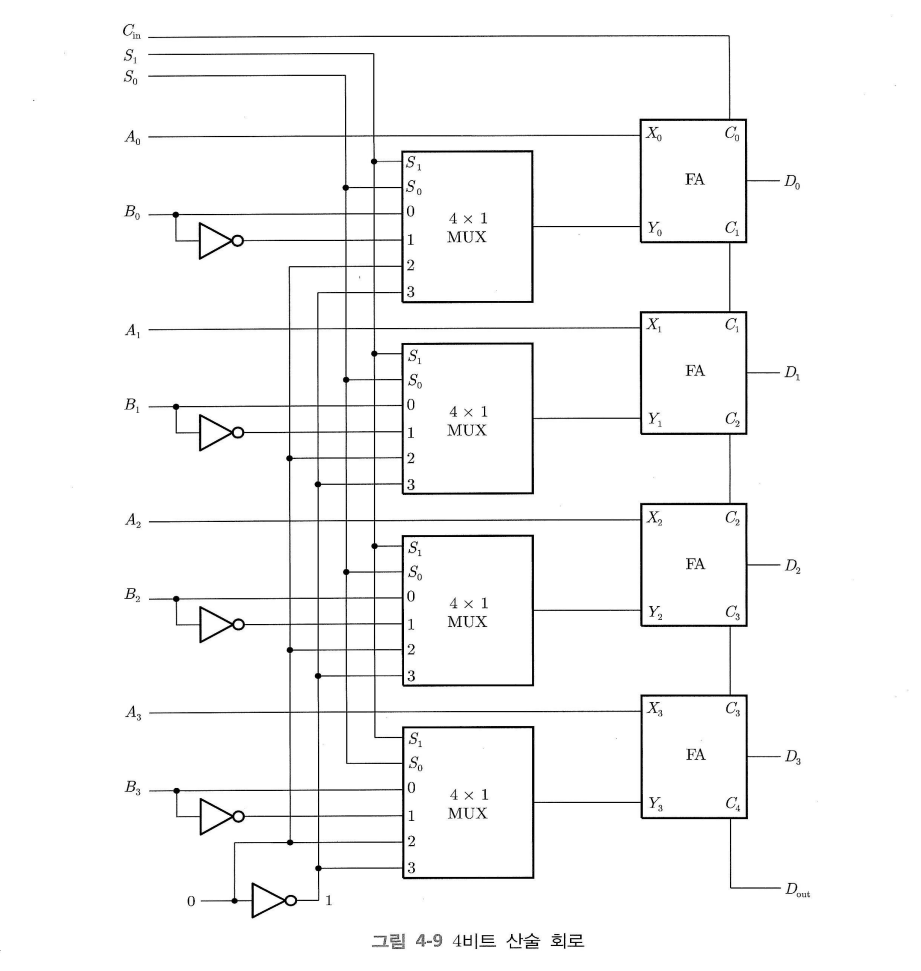
| $S_1$ | $S_0$ | $C_{in}$ | 입력 $Y$ | 출력 $D = A + Y + C_{in}$ | 마이크로연산 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | $B$ | $D = A + B$ | 덧셈 |
| 0 | 0 | 1 | $B$ | $D = A + B + 1$ | 캐리가 있는 덧셈 |
| 0 | 1 | 0 | $\overline{B}$ | $D = A + \overline{B}$ | 자리 내림을 고려한 뺄셈 |
| 0 | 1 | 1 | $\overline{B}$ | $D = A + \overline{B} + 1$ | 뺄셈 |
| 1 | 0 | 0 | 0 | $D = A$ | $A$ 전송 |
| 1 | 0 | 1 | 1 | $D = A + 1$ | $A$ 증가 |
| 1 | 1 | 0 | 1 | $D = A - 1$ | $A$ 감소 |
| 1 | 1 | 1 | 1 | $D = A$ | $A$ 전송 |
산술 마이크로 연산들을 병렬 가산기를 활용한 하나의 회로로 구현할 수 있다.
두 개의 4비트 입력인 A와 B, 그리고 출력 D가 존재한다.
선택 입력 두 개 $S_1, S_0$으로 출력을 선택한다.
논리 마이크로 연산
레지스터에 저장된 비트열에 대한 이진 연산이다.
\[P: R1 \leftarrow R1 \oplus R2\]$P=1$ 이후에 $R1$과 $R2$의 XOR 연산 결과가 $R1$에 저장된다.
| Boolean function | 마이크로연산 | 연산 이름 |
|---|---|---|
| $F_0 = 0$ | $F \leftarrow 0$ | 초기화 (Clear) |
| $F_1 = xy$ | $F \leftarrow A \land B$ | AND (논리곱) |
| $F_2 = x\overline{y}$ | $F \leftarrow A \land \overline{B}$ | |
| $F_3 = x$ | $F \leftarrow A$ | $A$ 전송 |
| $F_4 = x’ y$ | $F \leftarrow \overline{A} \land B$ | |
| $F_5 = y$ | $F \leftarrow B$ | $B$ 전송 |
| $F_6 = x \oplus y$ | $F \leftarrow A \oplus B$ | 배타적 논리합 (XOR) |
| $F_7 = x + y$ | $F \leftarrow A \lor B$ | OR (논리합) |
| $F_8 = (x + y)’$ | $F \leftarrow \overline{A \lor B}$ | NOR (논리합 부정) |
| $F_9 = (x \oplus y)’$ | $F \leftarrow \overline{A \oplus B}$ | 배타적 논리합 부정 (XNOR) |
| $F_{10} = y’$ | $F \leftarrow \overline{B}$ | $B$ 보수 (Complement) |
| $F_{11} = x + y’$ | $F \leftarrow A \lor \overline{B}$ | |
| $F_{12} = x’$ | $F \leftarrow \overline{A}$ | $A$ 보수 (Complement) |
| $F_{13} = x’ + y$ | $F \leftarrow \overline{A} \lor B$ | |
| $F_{14} = (xy)’$ | $F \leftarrow \overline{A \land B}$ | NAND (논리곱 부정) |
| $F_{15} = 1$ | $F \leftarrow \text{all 1’s}$ | 모든 비트를 1로 설정 |
하드웨어 구현

각 비트마다 논리 게이트가 필요하며, AND, OR, XOR, 보수 연산을 사용한다.
선택 신호에 따라 연산을 수행하여 멀티플렉서가 값을 선택한다.
$n$비트 데이터 처리를 위해 위 회로를 $n$개 반복한다.
응용
논리 마이크로 연산을 통해 특정 비트를 변경하거나 한 워드(word)의 일부분을 수정할 수 있다.
- selective-set 연산(=OR): B가 1인 부분을 A의 동일한 비트 위치에 1로 설정, 0이면 그대로
- selecitve-Complement 연산(=XOR): B가 1인 부분의 A의 비트를 보수로 바꿈
- selective-clear 연산(= AND + NOT): B의 1인 부분의 A 비트를 0으로
- mask 연산(= AND): B가 0인 부분을 A에서 0으로 변경
- insert 연산(= 마스킹 후 OR): B(mask) 값과 마스킹 후 B(insert) 값과 OR 연산
- clear 연산(= XOR): A, B 비교 후 동일한 비트는 0으로
시프트 마이크로 연산
| 기호적 표현 (Symbolic designation) | 설명 (Description) |
|---|---|
| $R \leftarrow shl \ R$ | 왼쪽 시프트 레지스터 $R$ |
| $R \leftarrow shr \ R$ | 오른쪽 시프트 레지스터 $R$ |
| $R \leftarrow cil \ R$ | 왼쪽 순환 시프트 레지스터 $R$ |
| $R \leftarrow cir \ R$ | 오른쪽 순환 시프트 레지스터 $R$ |
| $R \leftarrow ashl \ R$ | 산술 왼쪽 시프트 $R$ |
| $R \leftarrow ashr \ R$ | 산술 오른쪽 시프트 $R$ |
데이터 직렬 전송에 사용된다.
산술, 논리 연산이나 다른 데이터 처리 동작과 연계하여 사용될 수 있다.
레지스터의 값을 왼쪽 또는 오른쪽으로 이동(shift)시킨다.
순환 시프트(circular shift or rotate shift)
시프트된 비트를 반대쪽으로 순환하여 손실이 없다.
왼쪽 순환 시프트: $cil$
오른쪽 순환 시프트: $cir$
산술 시프트(arithmetic shift)
부호가 있는 정수 연산에 사용된다.
왼쪽 산술 시프트: 2배 곱하기
오른쪽 산술 시프트: 2로 나누기
부호 비트는 시프트되지 않아 변화가 없다.
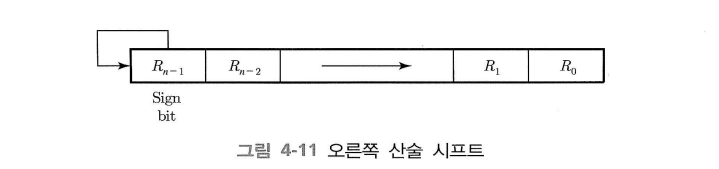
오른쪽 산술 시프트에서 $R_2$에서 $R_0$까지 오른쪽으로 시프트되어 $R_0$ 비트값을 잃어버린다.
왼쪽 산술 시프트에서는 $R_0$ 에 0을 삽입하고 나머지 상위 비트를 모두 왼쪽으로 시프트한다.
$R_{n-1}$ 값은 $R_{n-2}$로 치환되며, 오버플로가 일어날 수 있다.
하드웨어 구현
시프트 연산을 수행하려면 병렬 로드가 가능한 양방향 시프트 레지스터를 사용한다.
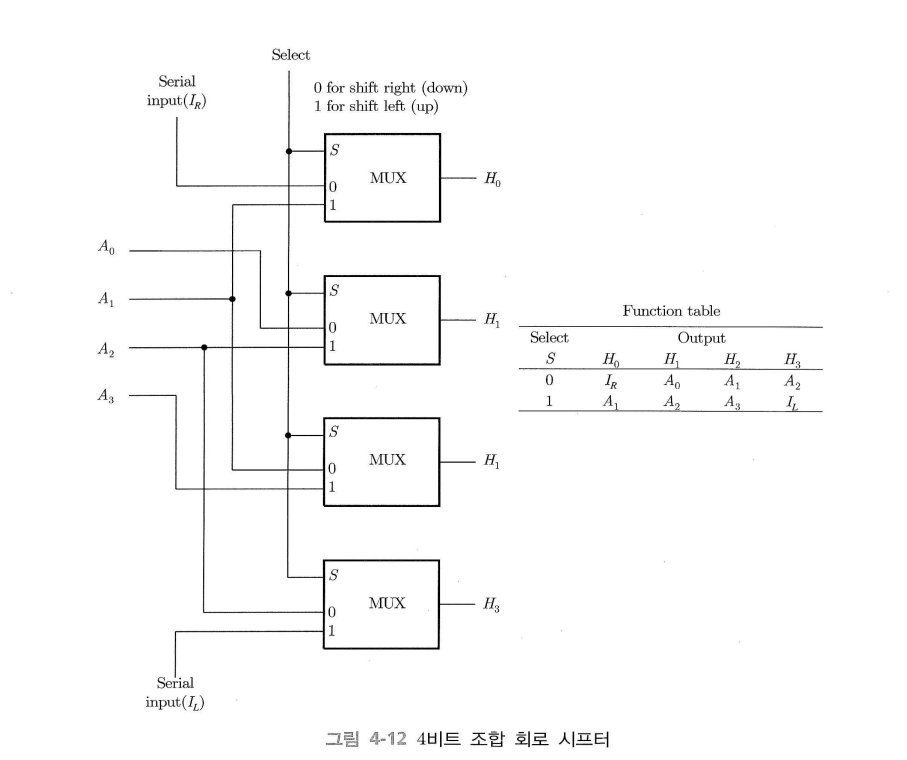
많은 레지스터를 가진 프로세서 장치에서는 조합 회로 시프터를 사용한다.
멀티플렉서를 이용하여 구현할 수 있다.
선택 신호 $S=0$이면 오른쪽으로 시프트, $S=1$이면 왼쪽 시프트이다.
산술 논리 시프트 장치
컴퓨터에서 산술 논리 장치(ALU)를 활용해 연산을 수행하고 전송한다.
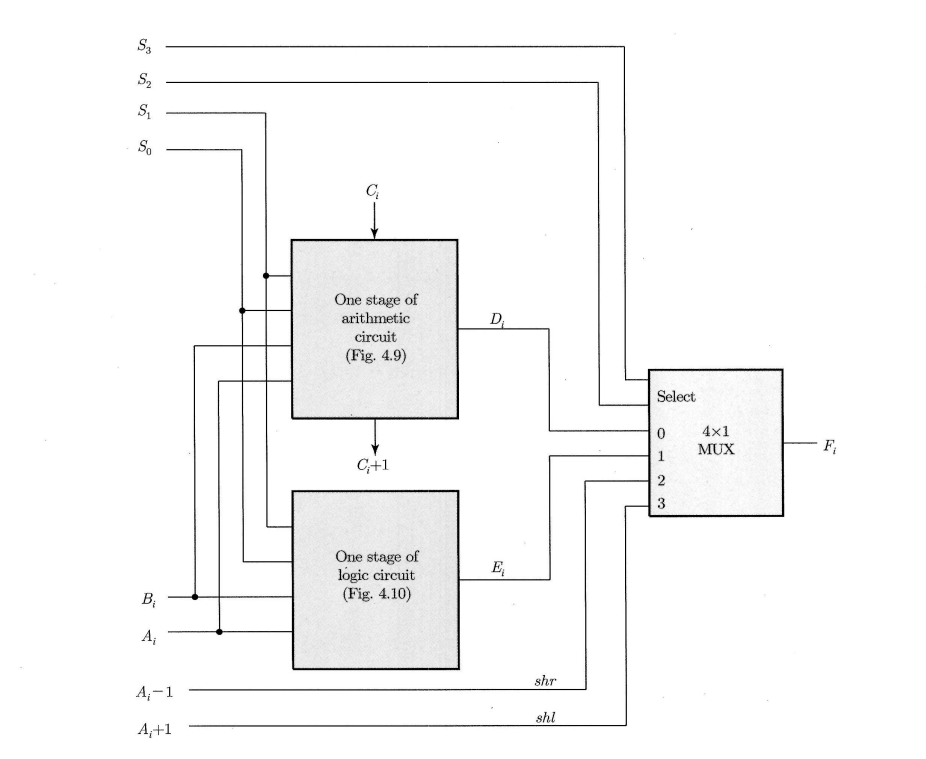
입력 $A_i$와 $B_i$는 산술 및 논리 장치와 연결된다.
선택 입력 $S_1$, $S_0$으로 마이크로 연산을 선택한다.
$S_3$, $S_4$는 시프트 연산을 위한 추가 신호이다.
$n$비트 ALU 구성을 위해 위와 같은 회로가 $n$개 필요한다.
| $S_3$ | $S_2$ | $S_1$ | $S_0$ | $C_{in}$ | 연산 (Operation) | 기능 (Function) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | $F = A$ | $A$ 전송 |
| 0 | 0 | 0 | 1 | 1 | $F = A + 1$ | $A$ 증가 (Increment) |
| 0 | 0 | 0 | 0 | 1 | $F = A + B$ | 덧셈 (Addition) |
| 0 | 0 | 0 | 1 | 1 | $F = A + B + 1$ | 캐리 포함 덧셈 |
| 0 | 0 | 1 | 0 | 0 | $F = A + \overline{B}$ | 자리 내림 포함 뺄셈 |
| 0 | 0 | 1 | 0 | 1 | $F = A + \overline{B} + 1$ | 뺄셈 |
| 0 | 0 | 1 | 1 | 0 | $F = A - 1$ | $A$ 감소 (Decrement) |
| 0 | 0 | 1 | 1 | 1 | $F = A$ | $A$ 전송 |
| 0 | 1 | 0 | 0 | × | $F = A \land B$ | 논리 AND |
| 0 | 1 | 0 | 1 | × | $F = A \lor B$ | 논리 OR |
| 0 | 1 | 1 | 0 | × | $F = A \oplus B$ | 논리 XOR |
| 0 | 1 | 1 | 1 | × | $F = \overline{A}$ | $A$ 보수 (Complement) |
| 1 | 0 | × | × | × | $F = shr A$ | $A$ 오른쪽 시프트 |
| 1 | 1 | × | × | × | $F = shl A$ | $A$ 왼쪽 시프트 |

댓글남기기