[밑바닥2] 4장 word2vec 속도 개선
Posted: Updated:
word2vec 속도 개선
단순한 2층 신경망으로 구현한 CBOW 모델은 코퍼스의 어휘 수가 많을 때 계산량도 커진다는 문제가 있다.
Embeddng 계층과 네거티브 샘플링을 통해 word2vec을 완성한다.
word2vec 개선 ①
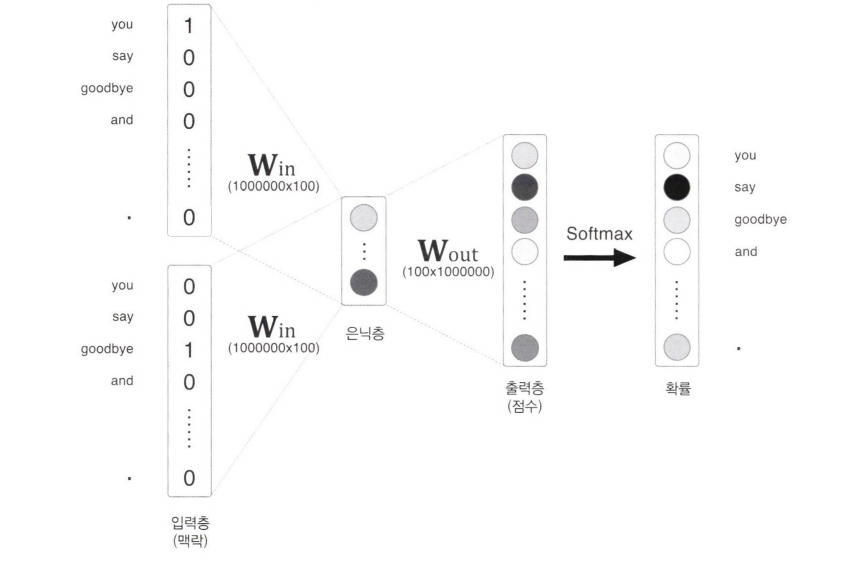
입력층과 출력층에 각 100만 개의 뉴런이 존재한다고 할 때, 다음의 두 계산이 병목되어 많은 시간이 소요된다.
입력층의 원 핫 표현과 가중치 행렬 $\mathrm{W_{in}}$ 의 곱 계산
단어를 원 핫 표현으로 다루기 때문에 어휘 수가 많아지면 원 핫 벡터의 크기도 커진다.
게다가 이 원 핫 벡터와 가중치 행렬 $\mathrm{W_{in}}$ 를 곱해야 한다.
Embedding 계층을 도입하여 이를 해결한다.
은닉층과 가중치 행렬 $\mathrm{W_{out}}$ 의 곱 및 Softmax 계층의 계산
*은닉층과 가중치 행렬 $\mathrm{W_{out}}$ 의 곱만 계산해도 계산량이 상당한데, Softmax 계층에서 다루는 어휘가 많아짐에 따라 계산량이 증가하는 문제가 있다.
네거티브 샘플링이라는 손실 함수를 도입해서 이를 해결한다.
Embedding 계층
기존 MatMul 계층의 행렬 곱 계산을 대체할 가중치 매개변수로부터 단어 ID에 해당하는 행(벡터)를 추출하는 계층인 Embedding 계층을 만든다.
Embedding 계층에 단어 임베딩(분산 표현)을 저장한다.
Embedding 계층 구현
특정 행을 추출하기 위해서는 원하는 행을 명시하면 된다.
import numpy as np
W = np.arange(21).reshape(7, 3)
W
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17],
[18, 19, 20]])
W[2]
array([6, 7, 8])
W[5]
array([l5, 16, 17])
배열을 통해 여러 행을 한꺼번에 추출할 수 있다.
idx = np.array([1, 0, 3, 0])
W[idx]
array([[ 3, 4, 5],
[ 0, 1, 2],
[ 9, 10, 11],
[ 0, 1, 2]])
Embedding 계층의 forward() 메서드는 아래와 같다.
class Embedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self, idx):
W = self.params
self.idx = idx
out = W[idx]
return out
역전파에서는 출력 측 층으로부터 전해진 기울기를 입력 층으로 그대로 흘려준다.
앞 층으로부터 전해진 기울기를 가중치 기울기 dW의 특정 행(idx번째 행)에 설정한다.
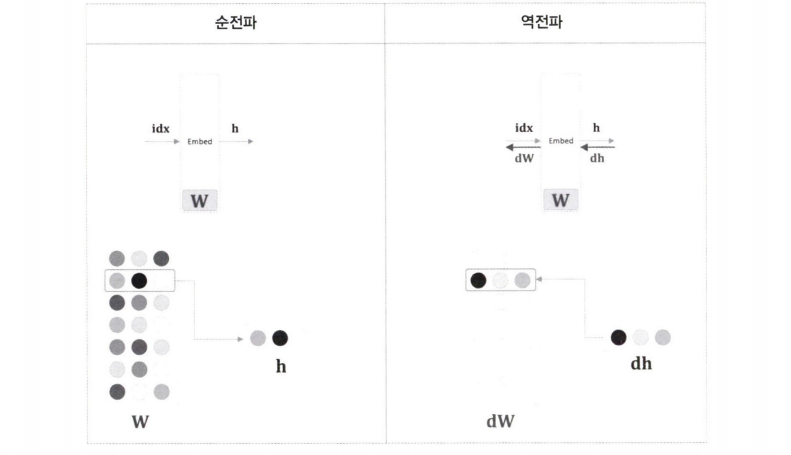
def backward(self, dout):
dW, = self.grads
dW[...] = 0
dW[self.idx] = dout
return None
dW의 형상을 유지한 채 원소를 0으로 초기화한다.
앞 층에서 전해진 기울기 dout을 idx번째 행에 할당한다.
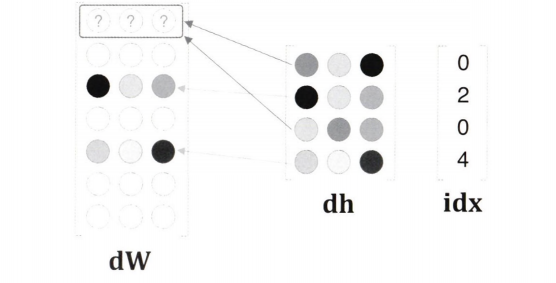
위와 같이 idx의 원소가 중복되는 경우 먼저 쓰여진 값을 덮어씌우게 된다.
따라서 할당이 아닌 더하기를 해야 한다.
dh의 각 행의 값을 dW의 해당 행에 더한다.
올바르게 구현한 예는 아래와 같다.
def backward(self, dout):
dW, = self.grads
dW[...] = 0
for i, word_id in enumerate(self.idx):
dW[word_id] += dout[i]
return None
for문 대신 넘파이의 np.add.at() 을 사용해도 된다.
np.add.at(A, idx, B) 는 B를 A의 idx번째 행에 더해준다.
word2vec 개선 ②
은닉층 이후 계산의 문제점
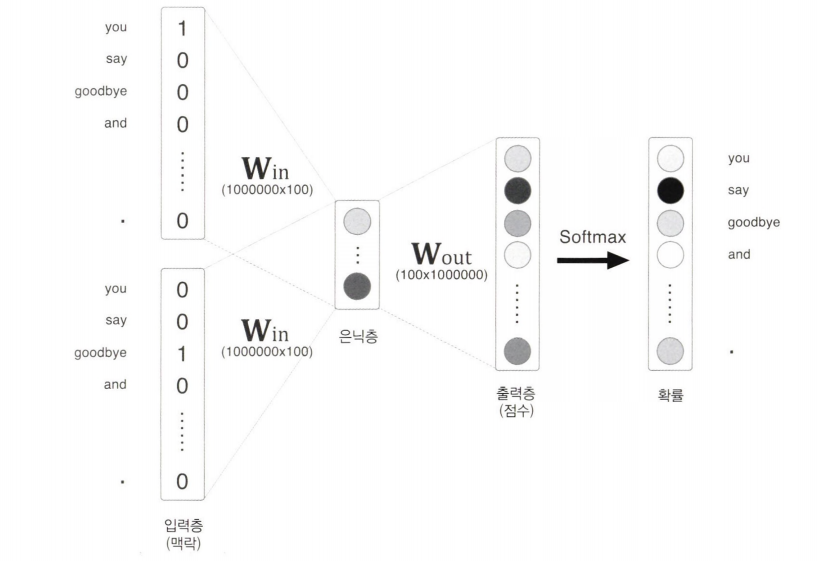
은닉층의 벡터 크기가 100이고, 가중치 행렬의 크기가 100 $\times$ 100만이므로, 계산이 오래 걸리고 메모리가 많이 필요하다.
역전파도 같은 계산을 수행하므로 행렬 곱을 가볍게 만들어야 한다.
위 식은 $k$ 번째 원소를 타깃으로 했을 때의 Softmax 계산식이다.
점수의 각 원소는 $(s_1, s_2, \cdots)$ 이다.
계산량이 어휘 수에 비례해 증가하므로 가벼운 계산이 필요하다.
다중 분류에서 이진 분류
다중 분류(multi-class classification)를 이진 분류로 근사하여 네거티브 샘플링을 이해해야 한다.
다중 분류 문제는 여러개의 답 중에서 옳은 답 하나를 선택하는 문제이고, 이진 분류는 “YES/NO”로 답하는 문제이다.
컨텍스트 “you”와 “goodbye”가 주어졌을 때 “say”의 확률이 높아지도록 하는 신경망이 아닌, 타깃 단어가 “say”인지 아닌지 묻는 질문에 답하는 신경망을 만들어야 한다.
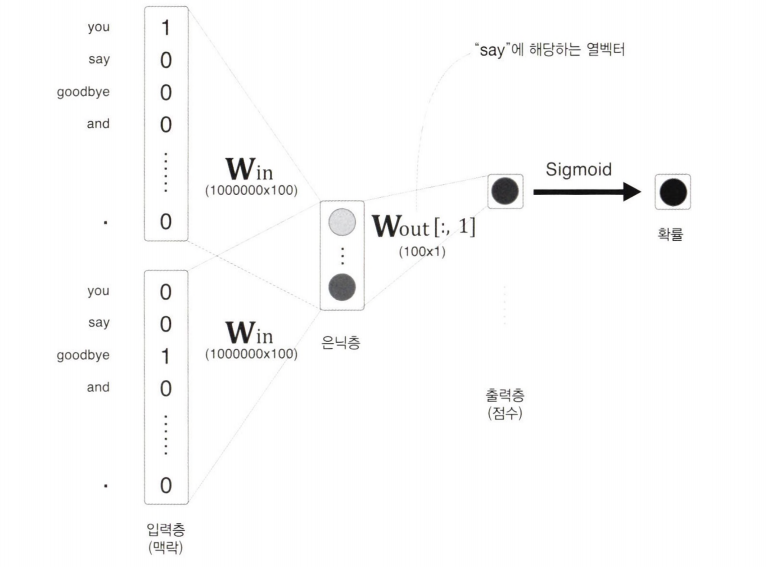
출력층에 뉴런을 하나 준비하여 “say”의 점수를 출력하게 한다.
출력층의 뉴런이 하나이므로, 은닉층과 출력 측의 가중치 행렬의 내적은 “say”에 해당하는 열(단어 벡터)만을 추출하고, 추출된 벡터와 은닉층 뉴런과의 내적을 계산하면 끝이다.
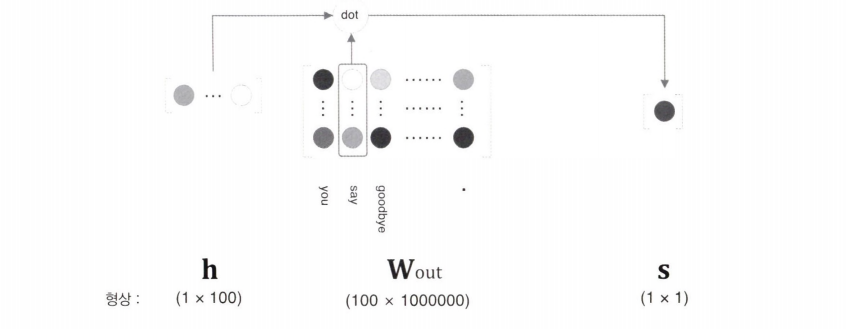
이전까지의 출력층에서는 모든 단어를 대상으로 계산을 수행했지만, 여기서는 “say”라는 단어 하나에 주목하여 계산하는 것이 핵심이다.
시그모이드 함수와 교차 엔트로피 오차
이진 분류 문제를 신경망으로 풀기 위해 점수에 시그모이드 함수를 적용해 확률로 변환한다.
손실을 구할 때는 교차 엔트로피 오차를 사용한다.
다중 분류의 경우 점수를 확률로 변환할 때는 소프트맥스 함수, 손실 함수는 교차 엔트로피 오차를 사용한다.
\[y = \frac {1} {1+\exp(-x)}\]시그모이드 함수는 위와 같다.
그래프는 S자 곡선이며, 입력값($x$)은 0에서 1 사이의 실수로 변환된다.
출력($y$)는 확률로 해석할 수 있다.
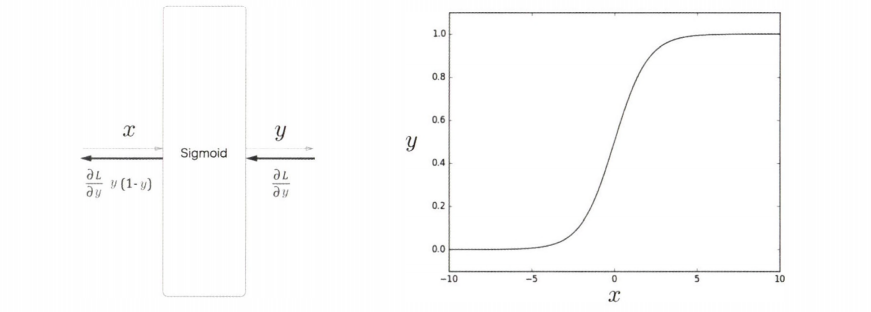
시그모이드 함수를 적용해 $y$를 얻고, 확률 $y$로부터 손실을 구한다.
시그모이드 함수에 교차 엔트로피 오차를 사용하면 아래와 같다.
$y$ 는 시그모이드 함수의 출력이고, $t$ 는 정답 레이블이다.
정답 레이블의 값은 0 또는 1이다.
$t$ 가 1이면 정답이 “Yes”이고, 0이면 “No”이다.
$t$ 가 1이면 $-\log y$ 가 출력되고, 반대로 $t$ 가 0이면 $-\log (1-y)$ 가 출력된다.
이진 분류와 다중 분류 모두 교차 엔트로피 오차를 사용하므로, Softmax with Loss 계층을 조금 수정해 Sigmoid with Loss 계층을 구현할 수 있다.
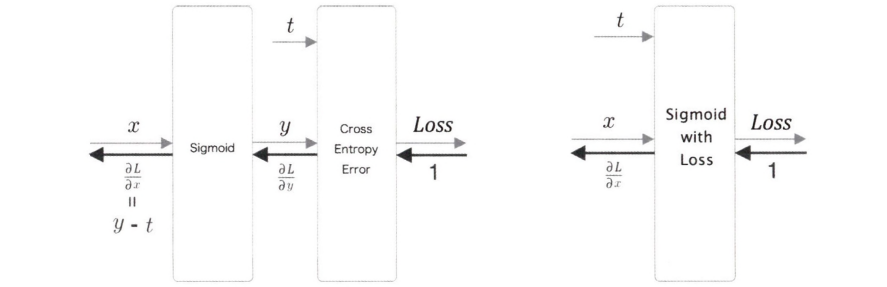
Sigmoid 계층과 Cross Entropy Error 계층의 계산 그래프이다.
Sigmoid 계층의 역전파는 $y-t$ 로 유도된다.
정답 레이블이 1이라면 $y$가 1에 가까워질수록 오차가 줄어든다.
오차가 앞 계층으로 흘러가므로 오차가 크먼 크게 학습하고, 오차가 작으면 작게 학습하게 된다.
다중 분류에서 이진 분류로 (구현)
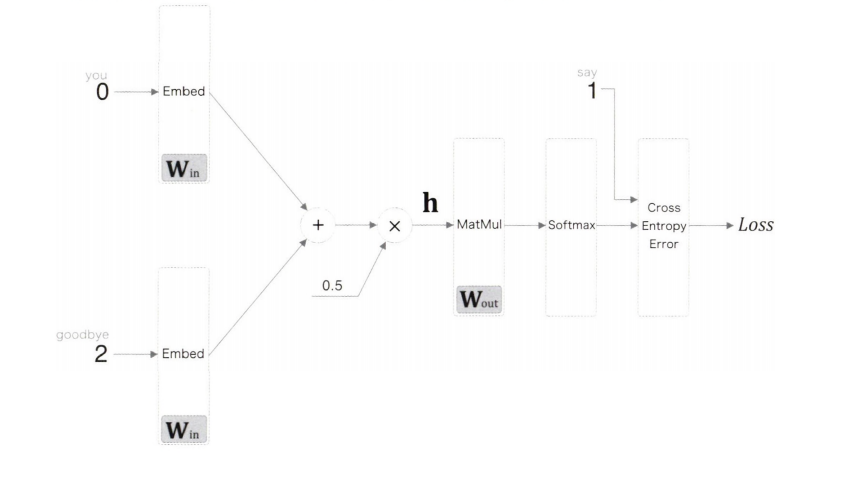
다중 분류를 수행하는 CBOW 모델의 전체 그림이다.
입력층에서는 각 단어 ID의 분산 표현을 추출하기 위해 Embedding 계층을 사용했다.
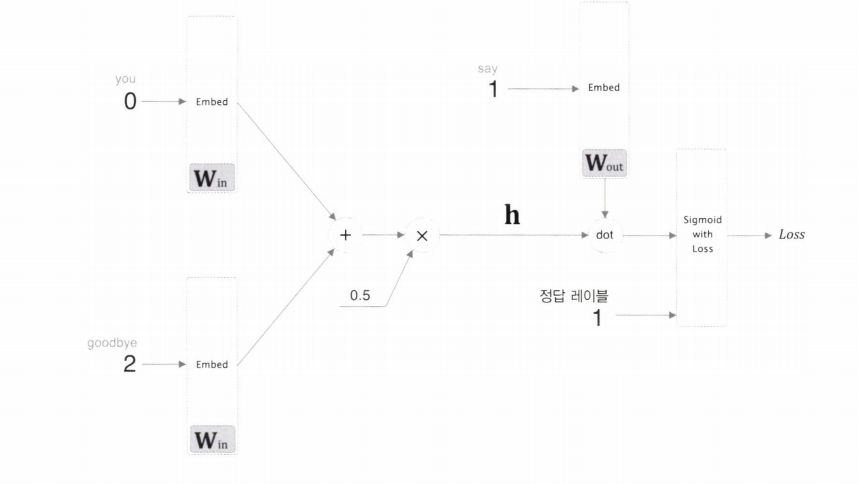
이진 분류 신경망으로 변환한 구성이다.
은닉층 뉴런 $\mathbf{h}$ 와,출력 측 가중치 $\mathrm{W_{out}}$ 에서 단어 “say”에 해당하는 단어 벡터와의 내적을 계산한다.
Embedding Dot 계층을 통해 후반부를 단순하게 만들 수 있다.
Embedding 계층과 dot 연산(내적) 처리를 합친 계층이다.
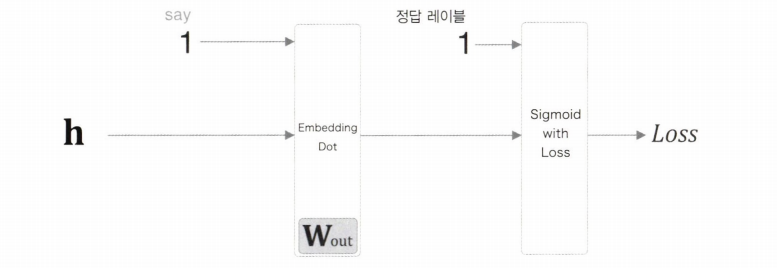
은닉층 뉴런 $\mathrm{h}$ 는 Embedding Dot 계층을 거쳐 Sigmoid with Loss 계층을 통과한다.
구현은 아래와 같다.
class EmbeddingDot:
def __init__(self, W):
self.embed = Embedding(W)
self.params = self.embed.params
self.grads = self.embed.grads
self.cache = None
def forward(self, h, idx):
target_W = self.embed.forward(idx)
out = np.sum(target_W * h, axis=1)
self.cache = (h, target_W)
return out
def backward(self, dout):
hz target_W = self.cache
dout = dout.reshape(dout.shape[0], 1)
dtarget_W = dout * h
self.embed.backward(dtarget_W)
dh = dout * target_W
return dh
인스턴스 변수가 embed, params, grads, cache로 총 4개 존재한다.
params 에는 매개변수, gards 에는 기울기를 저장한다.
embed 는 Embedding 계층이고, cache 는 순전파 시 계산 결과 유지하기 위한 변수이다.

forward(h, idx) 메서드는 은닉층 뉴런($h$)과 단어 ID의 넘파이 배열($idx$)을 받는다.
$idx$ 는 단어 ID의 배열로, 미니배치 처리를 가정한다.
Embedding 계층의 forward를 호출하여 내적을 계산한다.
네거티브 샘플링
지금까지 긍정적인 예(“say”)에 대해서만 학습했으므로 부정적인 예(“say” 이외)에 대해서는 학습하지 못했다.
긍정적 예에 대해서는 Sigmoid 계층의 출력을 1에 가깝게 만들고, 부정적인 예(“say” 이외)에 대해서는 Sigmoid 계층의 출력을 0에 가깝게 만들어야 한다.
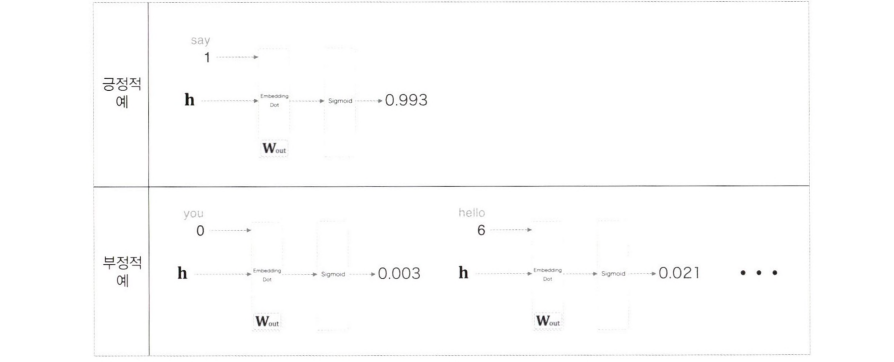
이러한 결과를 만들어주는 가중치가 필요하므로 적은 수의 부정적 예를 샘플링해 사용한다.
네거티브 샘플링 기법은 긍정적 예를 타깃으로 한 경우의 손실을 구한다.
이와 동시에 부정적 예를 몇 개 샘플링(선별)하여, 부정적 예에 대해서도 손실을 구한다.
긍정적 예와 샘플링된 부정적 예의 손실을 더한 값을 최종 손실로 한다.
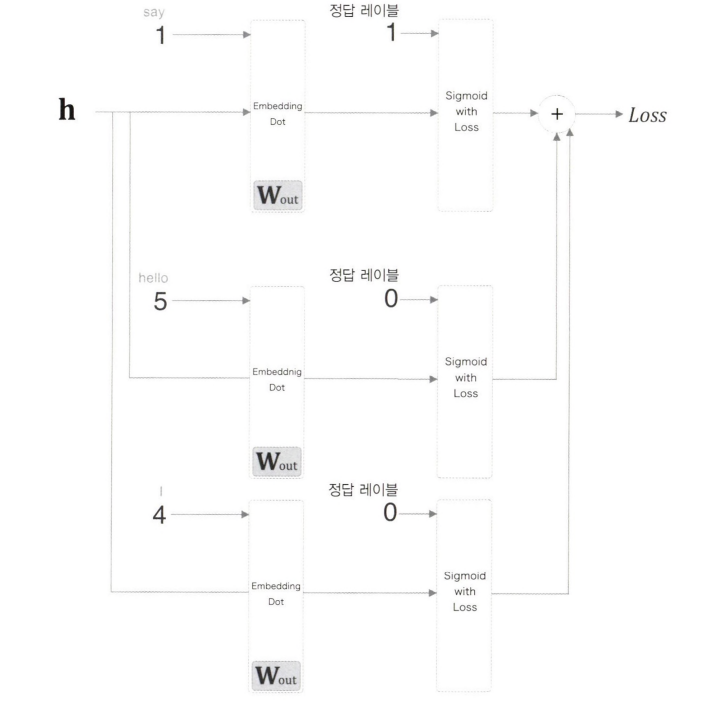
부정적 예의 타깃을 2개(“hello”와 “I”) 샘플링 했다고 가정할 때의 계산 그래프이다.
네거티브 샘플링의 샘플링 기법
부정적 예를 샘플링 할 때는 코퍼스의 통계 데이터를 활용하는 것이 좋다.
코퍼스에서 자주 등장하는 단어는 많이 추출하고, 적게 등장하는 단어는 적게 추출한다.
아래는 확률 분포에 따라 샘플링하는 코드이다.
import numpy as np
# 0~9 무작위 샘플링
np.random.choice(10)
7
# words 에서 하나 무작위 샘플링
words = ['you', 'say', 'goodbye', '1', 'hello', '.']
np.random.choice(words)
'goodbye'
# 중복 있는 5개 무작위 샘플링
np.random.choice(words, size=5)
array(['goodbye', '.', 'hello', 'goodbye', 'say'],
dtype='<U7')
# 중복 없는 5개 무작위 샘플링
np.random.choice(words, size=5, replace=False)
array(['hello', '.', 'goodbye', '1', 'you']
dtype='<U7')
# 확률 분포에 따른 샘플링
P = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
np.random.choice(words, p=p)
'you'
출현 확률이 낮은 단어를 버리지 않기 위해 기본 확률 분포에 0.75를 제곱한다.
\[P'(w_i) = \frac {P(w_i)^{0.75}} {\sum_j^n P(w_j)^{0.75}}\]수정 후에도 확률 총합이 1이 되어야 하므로, 분모로 수정 후 확률 분포의 총합이 필요하다.
P = [0.7, 0.29, 0.01]
new_p = np.power(p, 0.75)
new_p /= np.sum(new_p)
print(new.p)
[0.64196878 0.33150408 0.02652714]
수정 전 확률이 0.01이던 원소가 0.0265…로 높아졌다.
0.75라는 수치는 이론적인 의미가 없으니 다른 값으로 설정해도 된다.
유니그램(Unigram)이란 하나의 연속된 단어를 의미하고, 바이그램(Bigram)은 2개의 연속된 단어, 트라이그램(Trigram)은 3개의 연속된 단어를 뜻한다.
타깃 인수로 지정한 단어를 긍정적 예로 해석하고, 그 외의 단어 ID를 샘플링하는 get_negative_sample 메서드를 제공하는 UnigramSampler 클래스를 사용하는 코드이다.
corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size = 2
sampler = UnigramSampler(corpus, power, sample_size)
target = np.array([1, 3, 0])
negative_sample = sampler.get _negative_sample(target)
print(negative_sample)
# [[0 3]
# [1 2]
# [2 31]
긍정적 예로 [1, 3, 0]이라는 3개의 데이터를 미니배치로 다루고, 각 데이터에 대해 부정적 예를 2개식 샘플링한다.
네거티브 샘플링 구현
class NegativeSamplingLoss:
def __init__(self, W, corpus, power=0.75, sample_size=5):
self.sample_size = sample_size
self.sampler = UnigramSampler(corpus, power, sample_size)
self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]
self.params, self.grads =[], []
for layer in self.embed_dot_layers:
self.params += layer.params
self.grads += layer.grads
초기화 메서드의 인수는 출력 측 가중치를 나타내는 W , 단어 ID 리스트인 corpus , 확률분포에 제곱할 값인 power , 부정적 예의 샘플링 횟수인 sample_size 이다.
UnigramSampler 클래스로 인스턴스 변수 sampler 로 저장한다.
부정적 예의 샘플링 횟수는 sample_size 에 저장한다.
loss_layers 와 embed_dot_layers 에 원하는 계층을 리스트로 보관한다.
두 리스트에 긍정적 예를 다루는 계층이 하나 더 필요하므로 sample_size + 1 개의 계층을 생성한다.
이 계층에서 사용하는 매개변수와 기울기를 각각 배열로 저장한다.
def forward(self, h, target):
batch_size = target.shape[0]
negative_sample = self.sampler.get _negative_sample(target)
# 긍정적 예 순전파
score = self.embed_dot_layers[0].forward(h, target)
correct_label = np.ones(batch_size, dtype=np.int32)
loss = self.loss_layers[0].forward(score, correct_label)
# 부정적 예 순전파
negative_label = np.zeros(batch_size, dtype=np.int32)
for i in range(self.sample.size):
negative_target = negative_sample[:, i]
score = self.embed_dot_layers[1 + i].forward(h, negative_target)
loss += self.loss_layers[1 + i].forward(score, negative_label)
return loss
은닉층 뉴런 h 와 긍정적 예의 타깃을 뜻하는 target 을 인수로 받는다.
self.sampler 를 이용해 부정적 예를 샘플링해서 negative_sample 에 저장한다.
긍정적 예와 부정적 예 각각 데이터에 순전파를 수행하고 손실을 더한다.
def backward(self, dout=1):
dh = 0
for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
dscore = 10.backward(dout)
dh += l1.backward(dscore)
return dh
역전파는 순전파의 역순으로 backward() 를 호출하기만 하면 된다.
은닉층이 뉴런이 순전파 시 여러 개로 복사되었으므로, 역전파 때는 여러 개의 기울기 값을 더해준다.
개선판 word2vec 학습
CBOW 모델 구현
SimpleCBOW 클래스에 Embedding 계층과 Negative Sampling Loss 계층을 적용해 개선한다.
import sys
sys.path.append('..')
import numpy as np
from common.layers import Embedding
from ch04.negative_sampling_layer import NegativeSamplingLoss
class CBOW:
def __init__(self, vocab_size, hidden_size, window_size, corpus):
V, H = vocab_size, hidden_size
# 가중치 초기화
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(V, H).astype('f')
# 계층 생성
self.in_layers =[]
for i in range(2 * window_size):
layer = Embedding(W_in) # Embedding 계층 사용
self.in_layers.append(layer)
self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)
# 모든 가중치와 기울기 모으기
layers = self.in_layers + [self.ns_loss]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
# 단어의 분산 표현을 저장
self.word_vecs = W_in
def forward(self, contexts, target):
h = 0
for i, layer in enumerate(self.in_layers):
h += layer.forward(contexts[:, i])
h *= 1 / len(self.in_layers)
loss = self.ns_loss.forward(h, target)
return loss
def backward(self, dout=1):
dout = self.ns_loss. backward(dout)
dout *= 1 / len(self.in_layers)
for layer in self.in_layers:
layer.backward(dout)
return None
vocab_size 는 어휘 수, hidden_size 는 은닉층 뉴런 수, window_size 는 컨텍스트의 크기, corpus 는 단어 ID 목록이다.
NegativeSamplingLoss 계층에서 Embedding 계층을 사용하기 때문에, 출력 측 가중치와 입력 측 가중치가 같은 형상이고 단어 벡터가 행 방향에 배치된다.
순전파와 역전파는 각 계층의 순전파(혹은 역전파)를 적절한 순서로 호출하면 된다.
forward 메서드는 인수로 받는 컨텍스트와 타깃이 단어 ID이다.
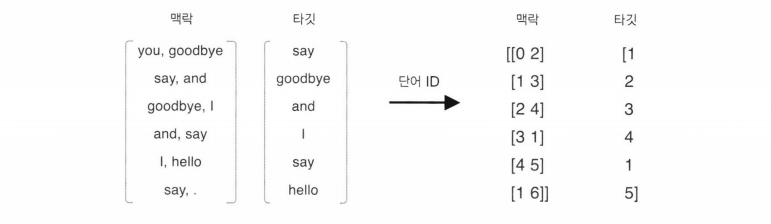
contexts 는 2차원 배열이고 target 은 1차원 배열이다.
CBOW 모델 학습 코드
import sys
sys.path.append('..')
import numpy as np
from common import config
# GPU에서 실행 시 아래 주석 해제 (쿠파이 필요)
# ===============================================
# config.GPU = True
# ===============================================
import pickle
from common.trainer import Trainer
from common.optimizer import Adam
from cbow import CBOW
from common.util import create_contexts_target, to_cpu, to_gpu
from dataset import ptb
window_size = 5
hidden_size = 100
batch_size = 100
max_epoch = 10
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
if config.GPU:
contexts, target = to_gpu(contexts), to_gpu(target)
model = CBOW(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()
word.vecs = model.word_vecs
if config.GPU:
word.vecs = to_cpu(word_vecs)
params = {}
params['word_vecs'] = word_vecs.astype(np.float16)
params['word_to_id'] = word_to_id
params['id_to_word'] = id_to_word
pkl_file = 'cbow_params.pkl'
with open(pkl_file, 'wb') as f:
pickle.dump(params, f, -1)
윈도우 크기를 2~10개, 은닉층의 뉴런 수는 50~500개 정도면 좋은 결과를 얻을 수 있다.
GPU로 실행하려면 윗쪽의 주석을 해제하면 된다.
단, 엔디비아 GPU를 장착한 컴퓨터여야 하고 쿠파이도 미리 설치해야 한다.
학습이 끝나면 가중치를 꺼내 나중에 이용할 수 있도록 파일에 보관한다.
파일로 저장 시 파이썬의 pickle 기능을 이용한다.
CBOW 모델 평가
import sys
sys.path.append('..')
from common.util import most_similar
import pickle
pkl_file = 'cbow_params.pkl'
with open(pkl_file, 'rb') as f:
params = pickle.load(f)
word_vecs = params['word_vecs']
word_to_id = params['word_to_id']
id_to_word = params['id_to_word']
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
most_similar(query, word_to_id, id_to_word, word_vecs, top=5)
[query] you
we: 0.610597074032
someone: 0.591710150242
i: 0.554366409779
something: 0.490028560162
anyone: 0.473472118378
[query] year
month: 0.718261063099
week: 0.652263045311
spring: 0.62699586153
summer: 0.625829637051
decade: 0.603022158146
[query] car
luxury: 0.497202396393
arabia: 0.478033810854
auto: 0.471043765545
disk-drive: 0.450782179832
travel: 0.40902107954
[query] toyota
ford: 0.550541639328
instrumentation: 0.510020911694
mazda: 0.49361255765
bethlehem: 0.474817842245
nissan: 0.474622786045
결과적으로 query 와 대략 비슷한 주제의 답변을 출력한다.
word2vec 으로 얻은 단어의 분산 표현은 비슷한 단어를 가까이 모을 뿐만 아니라 유추 문제(비유 문제)와 같이 더 복잡한 패턴을 파악할 수 있다.
king - man + woman = queen 처럼 유추 문제를 벡터의 덧셈과 뺄셈으로 풀 수 있다.
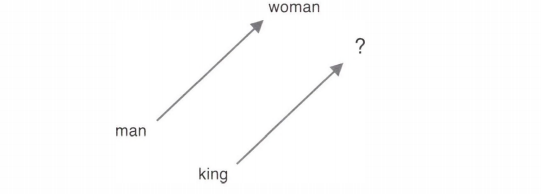
유추 문제를 풀기 위해 단어 벡터 공간에서 man —> woman 벡터와 king -> ? 벡터가 가능한 한 가까워지는 단어를 찾는다.
analogy 함수를 사용해서 한 줄로 처리할 수 있다.
analogy('man', 'king', 'woman', word_to_id, id_to_word, word_vecs, top=5)
[analogy] man:king = woman:?
wordl: 5.003233
word2: 4.400302
word3: 4.22342
word4: 4.003234
word5: 3.934550
문제 문장에 대한 점수가 높은 단어 5가지가 출력된다.
word2vec 남은 주제
word2vec을 사용한 애플리케이션의 예
전이 학습(transfer learning)이란 한 분야에서 배운 지식을 다른 분야에도 적용하는 기법이다.
자연어 문제를 풀 때는 위키백과나 구글 뉴스의 텍스트 데이터 등과 같이 큰 말뭉치로 먼저 학습한 다음 각자의 작업에 이용한다.
단어를 벡터로 변환하는 작업이 필요할 때 학습을 미리 끝낸 단어의 분산 표현을 이용할 수 있다.
단어의 분산 표현은 단어를 고정 길이 벡터로 변환해준다는 장점도 있다.
단어뿐만 아니라 문장도 고정 길이 벡터로 변환할 수 있다.
문장을 고정길이 벡터로 변환하는 방법 중 가장 간단한 방법은 문장의 각 단어를 분산 표현으로 변환하여 합을 구하는 것이다.
이를 bag-of-words 라고 하고, 단어의 순서를 고려하지 않는 모델이다.

자연어를 벡터로 변환하면 일반적인 머신러닝 기법을 적용시킬 수 있다.
자연어로 쓰여진 질문을 고정 길이 벡터로 변환하여 러신머닝 시스템의 입력으로 사용한다.
예를 들어 감정을 3단계로 분류해서 메일 자동 분류 시스템을 만든다고 하자.
데이터(메일)를 수집해서 모은 메일들에 수동으로 레이블을 붙인다.
레이블은 긍정적(positive), 중립적(neutral), 부정적(negative)이 존재한다.
레이블링이 끝나면 word2vec을 이용해 메일을 벡터로 변환한다.
이후 감정 분석을 수행하는 분류 시스템에 벡터화된 메일과 감정 레이블을 입력하여 학습을 수행한다.
단어 벡터 평가 방법
단어의 분산 표현의 우수성은 실제 애플리케이션과는 분리해서 평가한다.
이때 자주 평가되는 척도가 단어의 유사성이나 유추 문제를 활용한 평가이다.
유사성 평가는 사람이 작성한 단어 유사도를 검증 셋을 사용해 평가하는 것이 일반적이다.
유추 문제를 활용한 평가는 유추 문제의 정답률로 우수성을 측정한다.

댓글남기기