[밑바닥2] 5장 순환 신경망(RNN)
Posted: Updated:
순환 신경망 (RNN)
확률과 언어 모델
word2vec을 확률 관점에서 바라보다
$w_1, w_2, \cdots , w_T$ 라는 단어열로 표현되는 코퍼스에서, CBOW 모델은 컨텍스트의 단어로부터 타깃 단어를 추측한다.
$w_{t-1}$ 과 $w_{t+1}$ 이 주어졌을 때 타깃이 $w_t$ 가 될 확률은 아래와 같다.
CBOW 모델은 위 식의 사후 확률을 모델링한다.
사후 확률이란 $w_{t-1}$ 과 $w_{t+1}$ 이 주어졌을 때 $w_t$ 가 일어날 확률이다.
컨텍스트가 좌우 대칭이 아닌 경우, 예를 들어 왼쪽 두 단어만 컨텍스트로 생각하는 경우 CBOW 모델의 확률은 아래와 같이 달라진다.
\[{P(w_t \mid w_{t-2}, w_{t-1})}\]위 식을 이용해 CBOW 모델이 다루는 손실 함수를 교차 엔트로피 오차에 의해 아래와 같이 유도할 수 있다.
\[L = - \log P(w_t \mid w_{t-2}, w_{t-1})\]언어 모델
언어 모델(Language Model)은 단어 나열에 확률을 부여한다.
기계 번역, 음성 인식, 새로운 문장을 생성하는 용도로 이용된다.
언어 모델을 수식으로 설명할 수 있다.
$w_1, \cdots , w_m$ 이라는 $m$ 개의 단어로 된 문장이 있다고 할 때, 이 순서로 단어가 출현할 확률은 $P(w_1, \cdots , w_m)$ 로 나타낸다.
이 확률은 여러 사건이 동시에 일어날 확률이므로 동시 확률이라고 한다.
동시 확률 $P(w_1, \cdots , w_m)$ 은 사후 확률을 사용하여 아래와 같이 분해해서 쓸 수 있다.
\[\begin{matrix} P(w_1, \cdots, w_m) &=& P(w_m | w_1, \cdots, w_{m-1})P(w_{m-1} | w_1, \cdots, w_{m-2}) \\ && \cdots P(w_3 | w_1, w_2)P(w_2 | w_1)P(w_1) \\ &=& \prod_{i=1}^{m}P(w_i | w_1, \cdots, w_{i-1}) \end{matrix}\]동시 확률은 사후 확률의 총곱으로 나타낼 수 있다.
이 결과는 확률의 곱셈정리로부터 유도할 수 있다.
이는 A와 B가 모두 일어날 확률 $P(A, B)$ 가 B가 일어날 확률 $P(B)$와 B가 일어난 후 A가 일어날 확률 $P(A \mid B)$ 를 곱한 값과 같다는 것이다.
이 곱셈 정리를 사용해 $m$ 개 단어의 동시 확률을 사후 확률로 나타낼 수 있게 된다.
목적으로 하는 동시 확률은 사후 확률의 총곱인 $ \prod_{i=1}^{m}P(w_i \mid w_1, \cdots, w_{i-1}) $ 로 대표된다.
이 사후 확률은 타깃 단어보다 왼쪽에 있는 모든 단어를 컨텍스트로 했을 때의 확률이다.
따라서 $ P(w_t \mid w_1, w_2, \cdots, w_{t-1}) $ 을 구하면 언어 모델의 동시 확률 $P(w_1, \cdots, w_m)$ 를 구할 수 있다.
CBOW 모델을 언어 모델로?
CBOW 모델을 언어 모델에 적용하려면 컨텍스트의 크기를 특정 값으로 한정하여 근사적으로 나타낼 수 있다.
\[P(w_1, \ldots, w_m) = \prod_{i=1}^{m} P(w_i | w_1, \ldots, w_{i-1}) \approx \prod_{i=1}^{m} P(w_i | w_{i-2}, w_{i-1})\]여기서는 컨텍스트를 왼쪽 2개의 단어로 한정한다.
직전 2개의 단어에만 의존해 다음 단어가 정해지는 모델이므로 ‘2층 마르코프 연쇄’ 라고 부를 수 있다.
마르코프 연쇄(Markov Chain) 또는 마르코프 모델(Markov Model)은 미래의 상태가 현재 상태에만 의존해 결정되는 것을 말한다.
컨텍스트가 특정 길이로 고정되므로 더 왼쪽에 있는 단어는 무시되므로 문제가 발생할 수 있다. CBOW 모델의 컨텍스트를 얼마든지 키울 수 있지만, CBOW 모델에서는 맥락 안의 단어 순서가 무시된다.
따라서 컨텍스트의 단어 순서를 고려한 모델이 필요하다.
컨텍스트의 단어 벡터를 은닉층에서 연결(concatenate)하는 방식을 생각할 수 있다.
신경 확률론적 언어 모델(Neural Probabilistic Language Model)에서 제안한 방식은 이 방식을 취한다.
그러나 연결하는 방식을 취하면 컨텍스트의 크기에 비례해 가중치 매개변수도 늘어난다.
이를 해결하기 위해 순환 신경망(RNN)이 등장한다.
RNN은 컨텍스트가 아무리 길어도 정보를 기억하는 메커니즘을 갖추고 있다.
RNN이란
순환하는 신경망
순환하기 위해서는 닫힌 경로가 필요하다.
닫힌 경로 혹은 순환하는 경로가 존재해야 데이터가 같은 장소를 반복해 왕래할 수 있다.
RNN의 특징은 순환하는 경로가 있다는 것이다.
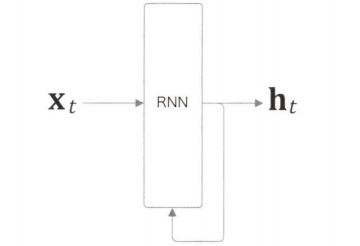
순환 경로를 따라 데이터를 계층 안에서 순환시킨다.
$\mathrm{x}_t$ 를 입력받는데, $t$ 는 시각을 뜻한다.
이는 시계열 데이터 $(\mathrm{x_0, x_1, \cdots , x_t , \cdots})$ 가 RNN 계층에 입력됨을 표현한 것이다.
그리고 입력에 대응하여 $(\mathrm{h_0, h_1, \cdots , h_t , \cdots})$ 가 출력된다.
각 시각에 입력되는 $\mathrm{x}_t$ 는 벡터라고 가정한다.
이 벡터가 순서대로 하나씩 RNN 계층에 입력된다.
위 그림에서 출력이 2개로 분기되는데, 같은 것이 복제되어 하나는 자기 자신에 입력되는 것이다.
순환 구조 펼치기

RNN 계층의 순환 구조를 피드포워드 신경망처럼 펼쳐서 표현할 수 있다.
각 시각의 RNN 계층은 그 계층으로의 입력과 1개 전의 RNN 계층으로부터의 출력을 받는다.
이 두 정보를 바탕으로 현 시각의 출력을 계산한다.
RNN에는 입력 $\mathrm{x}$ 를 출력 $\mathrm{h}$ 로 변환하기 위한 가중치 $\mathrm{W_x}$ 와 1개의 RNN 출력을 다음 시각의 출력으로 변환하기 위한 가중치 $\mathrm{W_h}$ , 편향 $b$ 가 있다.
$\mathrm{h}_{t-1}$ 과 $\mathrm{x}_t$ 는 행벡터이다.
이 식에서는 행렬 곱을 계산하고 그 합을 tanh 함수(쌍곡탄젠트 함수)를 이용해 변환한다.
RNN은 $\mathrm{h}$ 라는 상태를 가지고 있고, 위 식의 형태로 갱신된다고 해석할 수 있다.
따라서 RNN 계층을 상태를 가지는 계층 혹은 메모리(기억력)가 있는 계층이라고 한다.
$\mathrm{h}_t$ 를 은닉 상태(hidden state) 혹은 은닉 상태 벡터(hidden state vector)라고 한다.
BPTT

먼저 순전파를 수행하고 이어서 역전파를 수행해서 원하는 기울기를 구하는 오차역전파법을 적용할 수 있다.
여기서의 오차역전파법은 시간 방향으로 펼친 신경망의 오차역전파법이란 뜻으로 BPTT(Backpropagation Through Time)라고 한다.
매 시각 RNN 계층의 중간 데이터를 메모리에 유지해두어야 하므로 시계열 데이터의 시간 크기가 커지는 것에 비례하여 BPTT가 소비하는 컴퓨팅 자원이 늘어나는 문제가 있다.
또한, 시간 크기가 커지면 역전파 시 기울기가 불안정해지는 문제도 있다.
Truncated BPTT
Truncated BPTT는 시간축 방향으로 길어진 신경망을 적당한 지점에서 잘라내어 작은 신경망 여러개로 만들어 오차역전파법을 수행하는 방식이다.
역전파의 연결을 적당한 길이로 잘라내고 잘라낸 신경망 단위로 학습을 수행한다.
RNN에서 Truncated BPTT를 수행할 때는 데이터를 순서대로 입력해야 한다.
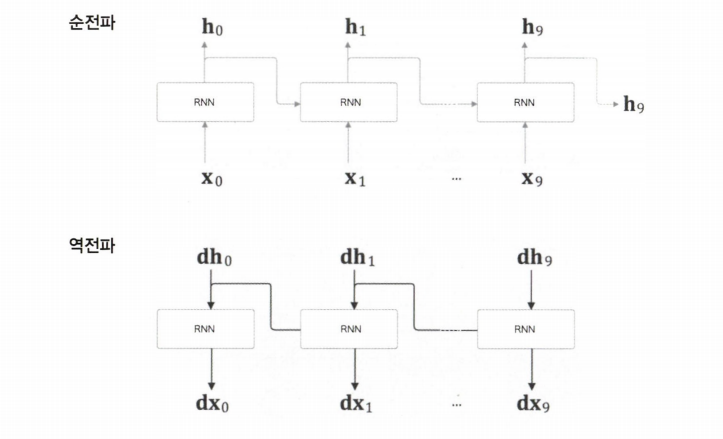
첫 번째 블록 입력 데이터 $(\mathrm{x_0, \cdots , x_9})$ 를 RNN 계층에 제공한 것이다.
순전파를 먼저 수행하고 역전파를 수행한다.
이 과정을 통해 원하는 기울기를 얻을 수 있다.
그리고 이어서 다음 블록의 입력 데이터$(\mathrm{x_{10}, \cdots , x_{19}})$를 입력해 오차역전파법을 수행한다.
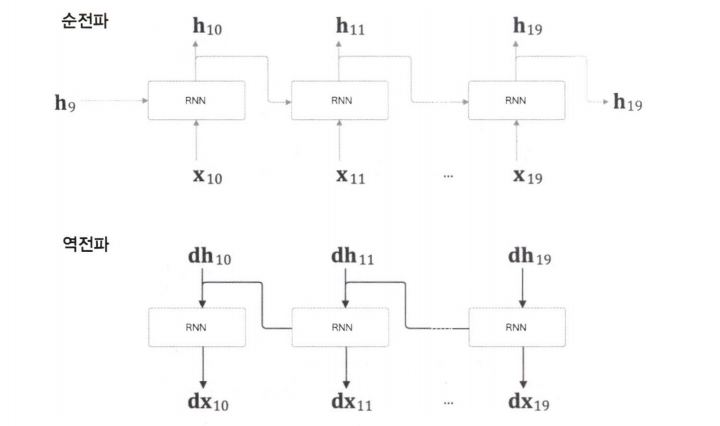
첫 번째 블록과 마찬가지로 순전파를 수행한 뒤 역전파를 수행하지만, 앞 블록의 마지막 은닉 상태인 $\mathrm{h_9}$ 가 필요하다.
Truncated BPTT의 미니배치 학습
미니배치 학습을 수행하기 위해서는 데이터를 주는 시작 위치를 각 미니배치의 시작 위치로 옮겨줘야 한다.
길이가 1,000인 시계열 데이터에 대해 미니배치의 수가 2일 경우, RNN 계층의 입력 데이터로 첫 번째 미니배치 때는 처음부터 순서대로 데이터를 제공하고, 두 번째 미니배치 때는 500번째의 데이터를 시작 위치로 정하고, 그 위치부터 다시 순서대로 데이터를 제공한다.
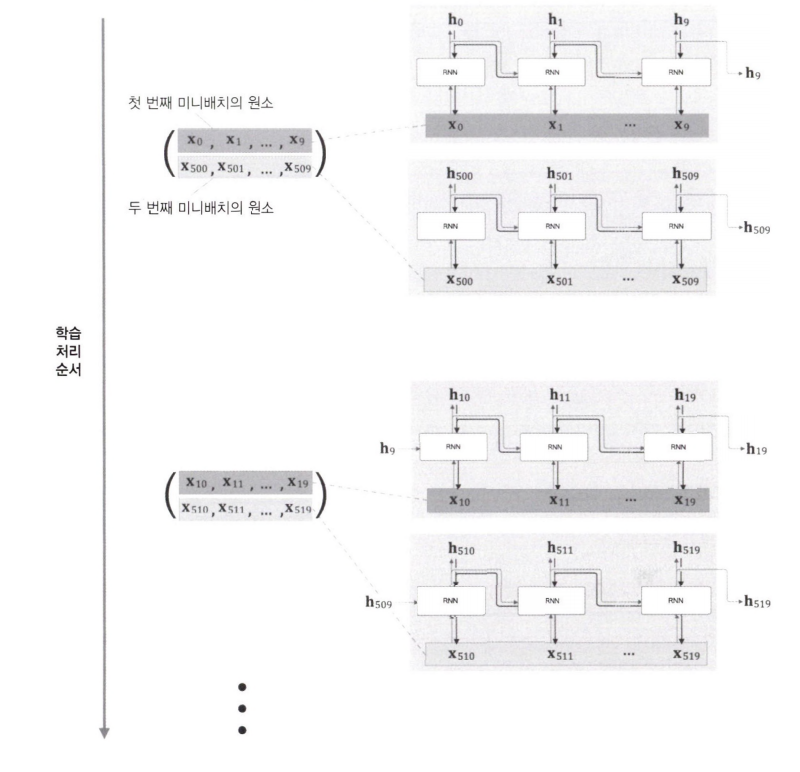
이처럼 미니배치 학습을 수행할 때는 각 미니배치의 시작 위치를 오프셋으로 옮겨준 후 순서대로 제공하면 된다.
데이터를 순서대로 입력하다가 끝에 도달하면 다시 처음부터 입력한다.
RNN 구현
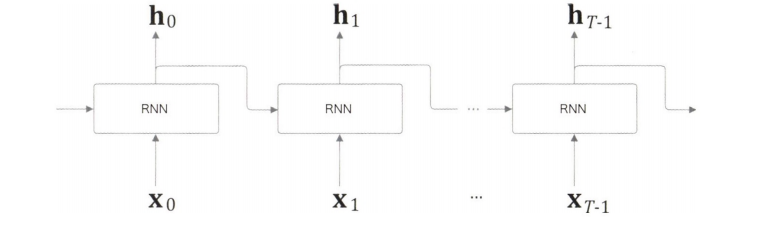
RNN에서 다루는 신경망은 위와 같다.
길이가 임의 값인 $T$ 시계열 데이터를 받는다.
각 시각의 은닉 상태를 $T$ 개 출력한다.
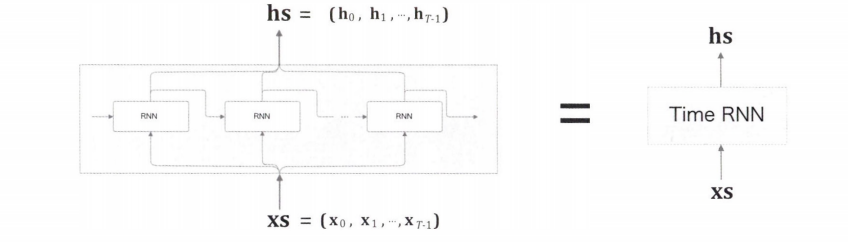
순환 구조를 펼친 후 계층들을 하나의 계층으로 간주하여 Time RNN 계층을 만든다.
이때 Time RNN 계층 내에서 한 단계 작업을 수행하는 계층을 RNN 계층이라고 한다.
$T$ 개 단계분의 작업을 한꺼번에 처리하는 계층을 Time RNN 계층이라 한다.
시계열 데이터를 한꺼번에 처리하는 계층 앞에 Time을 붙인다.
RNN 계층 구현
\[\mathrm{h}_t = \tanh (\mathrm{h}_{t-1} \mathrm{W_h+x}_t \mathrm{W_x+b})\]여기서 데이터를 미니배치로 모아 처리하기 때문에 $\mathrm{x}_t$ 와 $\mathrm{h}_t$ 에는 각 샘플 데이터를 행 방향에 저장한다.

미니배치 크기가 $N$ , 입력 벡터의 차원 수가 $D$ , 은닉 상태 벡터의 차원 수가 $H$ 일 때 형상을 확인한다.
형상 확인을 통해 올바르게 구현되었는지 확인한다.
class RNN:
def __init__(self, Wx, Wh, b):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = None
def forward(self, x, h_prev):
Wx, Wh, b = self.params
t = np.matmul(h_prev, Wh) + np.matmul(x, Wx) + b
h_next = np.tanh(t)
self.cache = (x, h_prev, h_next)
return h_next
RNN 클래스의 초기화와 순전파 메서드이다.
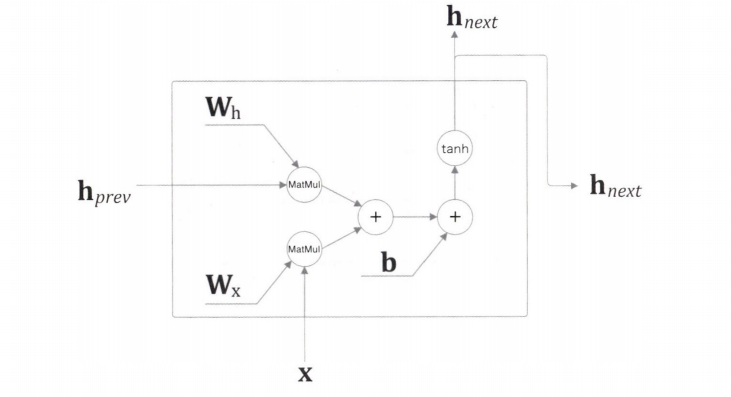
RNN의 순전파를 계산 그래프로 나타낸 것이다.
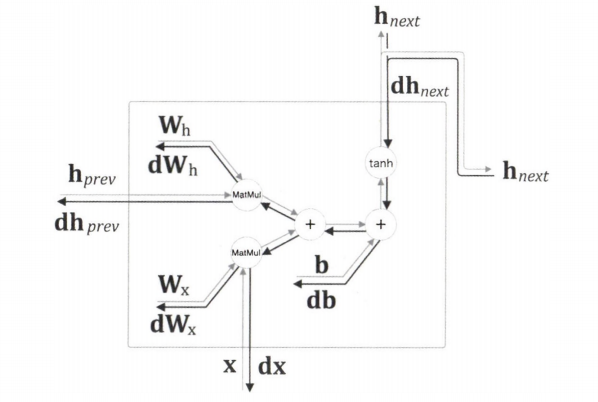
역전파를 포함한 RNN 계층의 계산 그래프이다.
아래는 RNN 계층의 역전파 구현이다.
def backward(self, dh_next):
Wx, Wh, b = self.params
xz h_prev, h_next = self.cache
dt = dh_next * (1 - h_next ** 2)
db = np.sum(dt, axis=0)
dWh = np.matmul(h_prev.T, dt)
dh_prev = np.matmul(dt, Wh.T)
dWx = np.matmul(x.T, dt)
dx = np.matmul(dt, Wx.T)
self.grads[0][...] = dWx
self.grads[l][...] = dWh
self.grads[2][...] = db
return dx, dh_prev
Time RNN 계층 구현
Time RNN 계층은 RNN 계층 $T$ 개를 연결한 신경망이다.
RNN 계층의 은닉 상태 h를 인스턴스 변수로 유지하고, 은닉 상태를 인계받는 데 사용한다.
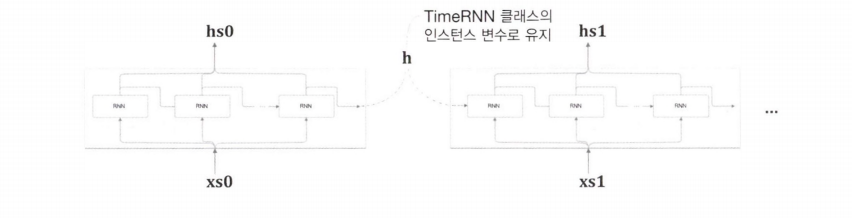
RNN 계층의 은닉 상태를 Time RNN 계층에서 관리한다.
그리고 이 기능을 stateful 이라는 인수로 조정하도록 한다.
class TimeRNN:
def __init__(self, Wx, Wh, b, stateful=False):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.dh = None, None
self.stateful = stateful
def set_state(self, h):
self.h = h
def reset_state(self):
self.h = None
layers 변수에 다수의 RNN 계층을 리스트로 저장한다.
인스턴스 변수 h 에 forward() 메서드를 불렀을 때 마지막 RNN 계층의 은닉 상태를 저장한다.
dh 는 backward() 를 불렀을 때 하나 앞 블록의 은닉 상태의 기울기를 저장한다.
stateful 이 True 일 때, Time RNN 계층은 아무리 긴 시계열 데이터라도 순전파를 끊지 않고 전파한다.
False 일 때, Time RNN 계층은 상태가 없는 무상태로 초기화 하기 위해 은닉 상태를 영행렬로 초기화한다.
def forward(self, xs):
Wx, Wh, b = self.params
N, T, D = xs.shape
D, H = Wx.shape
self.layers = []
hs = np.empty((N, T, H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
for t in range(T):
layer = RNN(*self.params)
self.h = layer.forward(xs[:, t, :], self.h)
hs[:, t, :] = self.h
self.layers.append(layer)
return hs
xs 는 T개 분량의 시계열 데이터를 하나로 모은 것이다.
미니배치 크기가 N, 입력 벡터의 차원 수가 D라면, xs의 형상은 (N, T, D)가 된다.
RNN 계층의 은닉 상태 h는 처음 호출 시 원소가 모두 0인 영행렬로 초기화되며, 인스턴스 stateful 이 False 일 때도 영행렬로 초기화된다.
forward() 메서드가 호출되면 인스턴스 변수 h 에 마지막 RNN 계층의 은닉 상태가 저장된다.
다음 번 forward() 메서드 호출 시 stateful이 True면 먼저 저장된 h가 그대로 이용되고, False면 영행렬로 초기화된다.
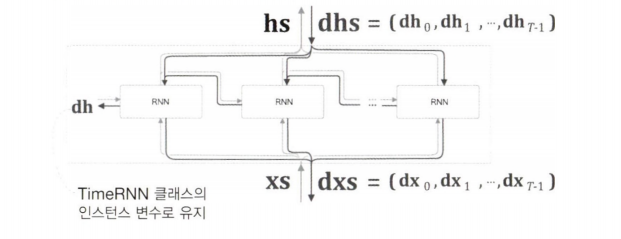
Time RNN 계층의 역전파 계산 그래프이다.
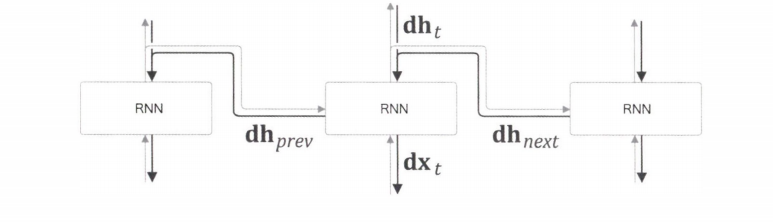
$t$ 번째 RNN 계층에 주목한 역전파 그림이다.
순전파에서는 출력이 2개로 분기되고, 순전파에서 분기했을 경우 역전파에서는 각 기울기가 합산되어 전해진다.
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D, H = Wx.shape
dxs = np.empty((N, T, D), dtype='f')
dh = 0
grads = [0, 0, 0]
for t in reversed(range(T)):
layer = self.layers[t]
dx, dh = layer.backward(dhs[:, t, :] + dh) # 합산된 기울기
dxs[:, t,:] = dx
for i, grad in enumerate(layer.grads):
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs
시계열 데이터 처리 계층 구현
RNNLM의 전체 그림
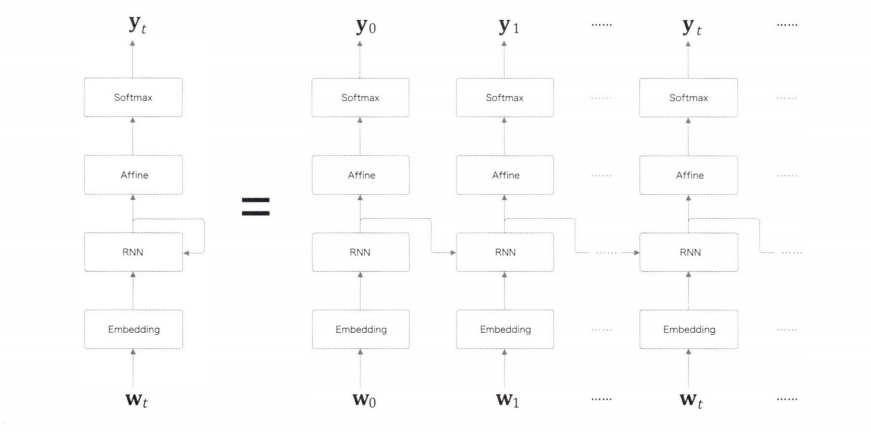
“you say goodbye and I say hello.” 를 처리하는 RNNLM 은 아래와 같다.
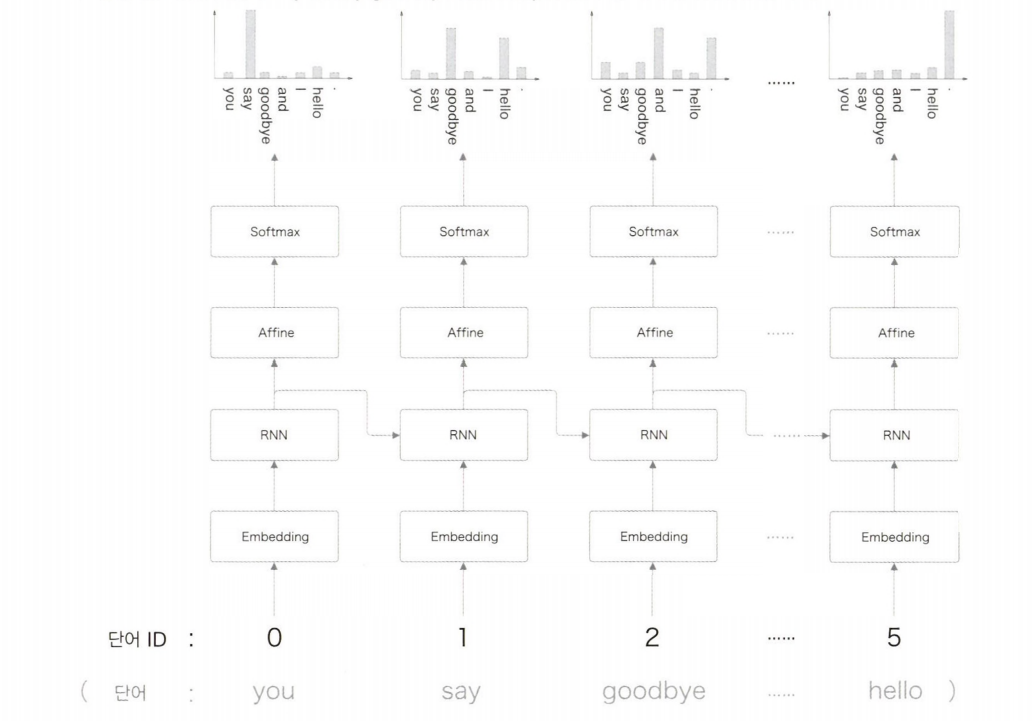
RNNLM은 지금까지 입력된 단어를 기억하고, 이를 바탕으로 다음에 출현할 단어를 예측한다.
RNN 계층을 통해 과거에서 현재로 데이터를 흘려보내줌으로써 과거의 정보를 인코딩해 저장할 수 있다.
Time 계층 구현
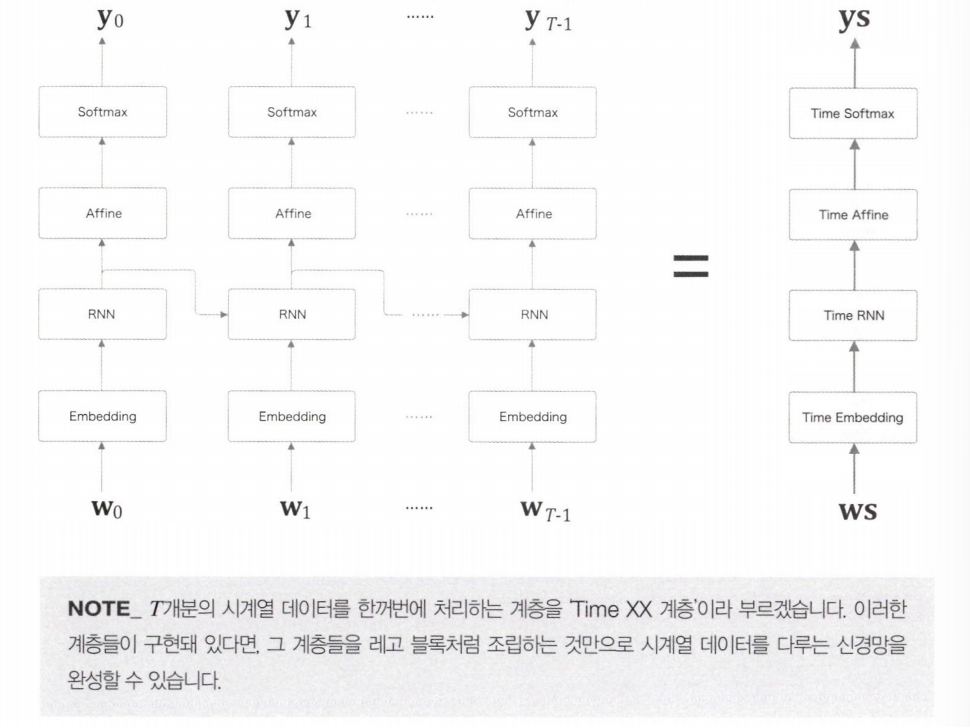
시계열 데이터를 한꺼번에 처리하는 계층을 Time Embedding, Time Affine 형태의 이름으로 구현한 그림이다.
Time Affine 계층은 Affine 계층을 $T$ 개 준비해서, 각 시각의 데이터를 개별적으로 처리하면 된다.
Time Embedding 계층 역시 순전파 시에 $T$ 개의 Embedding 계층을 준비하고 각 Embedding 계층이 각 시각의 데이터를 처리한다.
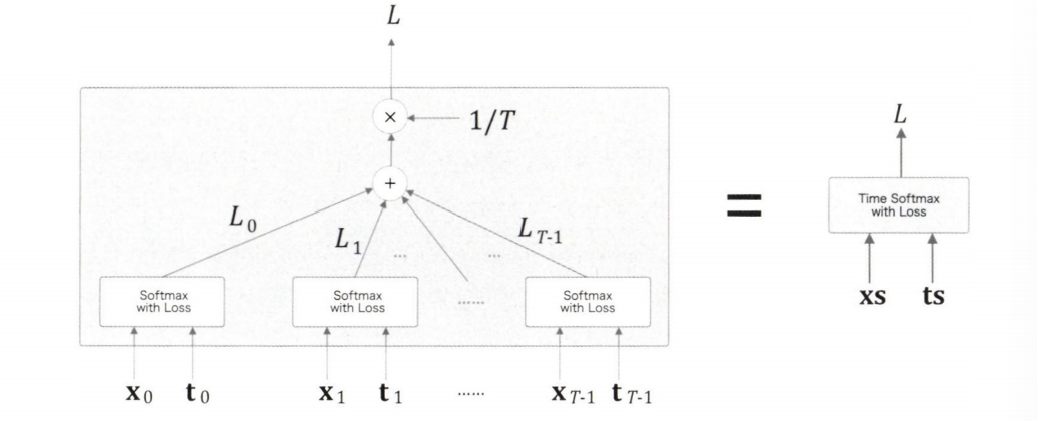
time softmax with loss 계층의 전체 그림이다.
$\mathrm{x}_0$ 나 $\mathrm{x}_1$ 등의 데이터는 확률로 정규화되기 전의 값인 아래층에서부터 전해지는 점수를 나타낸다.
$\mathrm{t}_0$ 나 $\mathrm{t}_1$ 등의 데이터는 정답 레이블을 나타낸다.
$T$ 개의 Softmax with Loss 계층 각각이 손실을 산출한다.
손실들을 합산해 평균한 값이 최종 손실이 되고, 이때 수행하는 계산의 수식은 위와 같다.

댓글남기기